题目内容
2. 在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高,动点P从点A出发,沿A→D方向以$\sqrt{2}$cm/s的速度向点D运动.设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间为t秒,则t=6秒时,S1=2S2.
在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高,动点P从点A出发,沿A→D方向以$\sqrt{2}$cm/s的速度向点D运动.设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间为t秒,则t=6秒时,S1=2S2.
分析 利用三角形的面积公式以及矩形的面积公式,表示出S1和S2,然后根据S1=2S2,即可列方程求解.
解答 解:∵Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高,
∴AD=BD=CD=8$\sqrt{2}$cm,
又∵AP=$\sqrt{2}$t,
则S1=$\frac{1}{2}$AP•BD=$\frac{1}{2}$×8$\sqrt{2}$×$\sqrt{2}$t=8t,PD=8$\sqrt{2}$-$\sqrt{2}$t,
∵PE∥BC,
∴△APE∽△ADC,
∴$\frac{PE}{DC}$=$\frac{AP}{AD}$,
∴PE=AP=$\sqrt{2}$t,
∴S2=PD•PE=(8$\sqrt{2}$-$\sqrt{2}$t)•$\sqrt{2}$t,
∵S1=2S2,
∴8t=2(8$\sqrt{2}$-$\sqrt{2}$t)•$\sqrt{2}$t,
解得:t=6.
故答案是:6.
点评 本题考查了一元二次方程的应用,以及等腰直角三角形的性质,正确表示出S1和S2是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.若方程$\frac{3-2x}{x-3}$+$\frac{2+mx}{3-x}$=-1无解,则m的值是( )
| A. | -1 | B. | 3 | C. | -1或3 | D. | -1或-$\frac{5}{3}$ |
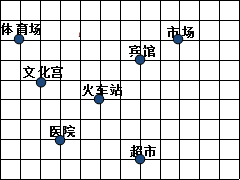 如图,这是某市部分简图,请按要求画出平面直角坐标系,分别写出各地的坐标.
如图,这是某市部分简图,请按要求画出平面直角坐标系,分别写出各地的坐标.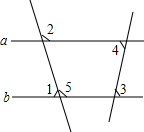 如图,已知∠1=80°,∠2=100°,∠3=85°,求∠4的度数.
如图,已知∠1=80°,∠2=100°,∠3=85°,求∠4的度数.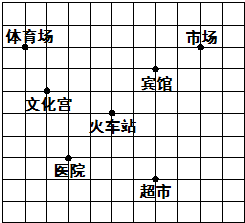 如图(小方格的边长为1),这是某市部分简图.
如图(小方格的边长为1),这是某市部分简图.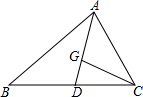 如图,在△ABC中,G是重心,点D是BC的中点,若△ABC的面积为6cm2,则△CGD的面积为1cm2.
如图,在△ABC中,G是重心,点D是BC的中点,若△ABC的面积为6cm2,则△CGD的面积为1cm2. 如图,AB∥CD∥EG,AC∥DF,若∠BAC=120°,则∠CDF=60°.
如图,AB∥CD∥EG,AC∥DF,若∠BAC=120°,则∠CDF=60°.