题目内容
12.代数式2x2-3x+1的最小值是-$\frac{1}{8}$.分析 先利用配方法将代数式2x2-3x+1转化为完全平方与数字的形式,然后根据非负数的性质进行解答.
解答 解:2x2-3x+1
=2(x2-$\frac{3}{2}$x+$\frac{9}{16}$)-2×$\frac{9}{16}$+1
=2(x-$\frac{3}{4}$)2-$\frac{1}{8}$.
∵2(x-$\frac{3}{4}$)2≥0,
∴2x2-3x+1的最小值是-$\frac{1}{8}$.
故答案是:-$\frac{1}{8}$.
点评 本题考查了配方法的应用.解题时要注意配方法的步骤.注意在变形的过程中不要改变式子的值.

练习册系列答案
相关题目
2.下列方程中,有实数根的方程是( )
| A. | x4+3=0 | B. | $\sqrt{x-2}$=-1 | C. | $\frac{x}{{x}^{2}-1}$=$\frac{1}{{x}^{2}-1}$ | D. | $\sqrt{x+1}$=-x |
17.计算(-$\sqrt{2015}$)2( )
| A. | 2015 | B. | -2015 | C. | ±2015 | D. | 20152 |
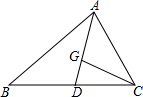 如图,在△ABC中,G是重心,点D是BC的中点,若△ABC的面积为6cm2,则△CGD的面积为1cm2.
如图,在△ABC中,G是重心,点D是BC的中点,若△ABC的面积为6cm2,则△CGD的面积为1cm2. 如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,求∠DAC度数.
如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,求∠DAC度数.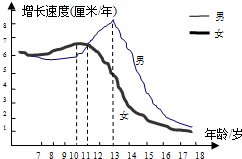 生物学研究表明在8-17岁期间,男女生身高增长速度规律呈现如图所示,请你观察此图,回答下列问题:男生身高增长速度的巅峰期是13岁,在11岁时男生女生的身高增长速度是一样的.
生物学研究表明在8-17岁期间,男女生身高增长速度规律呈现如图所示,请你观察此图,回答下列问题:男生身高增长速度的巅峰期是13岁,在11岁时男生女生的身高增长速度是一样的.