题目内容
14.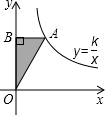 如图,点A是反比例函数y=$\frac{k}{x}$(k≠0)图象上一点,AB⊥y轴,垂足为点B,S△AOB=3,则以下结论:
如图,点A是反比例函数y=$\frac{k}{x}$(k≠0)图象上一点,AB⊥y轴,垂足为点B,S△AOB=3,则以下结论:①常数k=3;
②在每个象限内,y随x的增大而减小;
③当y>2时,x的取值范围是x<3;
④若点D(a,b)在图象上,则点D′(b,a)也在图象上.其中正确的是( )
| A. | ①② | B. | ③④ | C. | ②④ | D. | ①③ |
分析 根据S△AOB=3,可知k=6,故①错误;根据k的值可知在每个象限内,y随x的增大而减小,故②正确;先求出y=2时,x的值,再由函数增减性可知0<x<3,故③错误;根据反比例函数图象上点的坐标特点可知④正确.
解答 解:①∵AB⊥y轴,垂足为点B,S△AOB=3,
∴k=6,故①错误;
②∵k=6>0,
∴函数图象的两个分支分别位于一三象限,
∴在每个象限内,y随x的增大而减小,故②正确;
③∵y=2时,2=$\frac{6}{x}$,解得x=3,
∴当y>2时,x的取值范围是0<x<3,故③错误;
④∵ab=ba,
∴若点D(a,b)在图象上,则点D′(b,a)也在图象上,故④正确.
故选C.
点评 本题考查的是反比例函数的性质,熟知反比例函数系数k的几何意义及反比例函数的增减性是解答此题的关键.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
4.已知点A(-3,m)与点B(2,n)是直线y=-$\frac{2}{3}$x+b上的两点,则m与n的大小关系是( )
| A. | m>n | B. | m=n | C. | m<n | D. | 无法确定 |
5.若|1-x|+$\sqrt{x-1}$=0,则x的取值范围是( )
| A. | x≥1 | B. | x=1 | C. | x≤1 | D. | x>1 |
9.立定跳远是小刚同学体育中考的选考项目之一.某次体育课上,体育老师记录了小刚的一组立定跳远训练成绩如下表:
则下列关于这组数据的说法中正确的是( )
| 成绩(m) | 2.35 | 2.4 | 2.45 | 2.5 | 2.55 |
| 次数 | 1 | 1 | 2 | 5 | 1 |
| A. | 众数是2.45 | B. | 平均数是2.45 | C. | 中位数是2.5 | D. | 方差是0.48 |
 在平面直角坐标系中,已知点A(-2,1),B(-1,0),C(0,1),请在图中画出△ABC,并画出与△ABC关于原点O对称的△A1B1C1.
在平面直角坐标系中,已知点A(-2,1),B(-1,0),C(0,1),请在图中画出△ABC,并画出与△ABC关于原点O对称的△A1B1C1.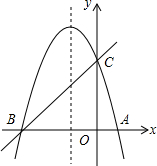 如图,已知抛物线y=ax2+bx+c(a≠0)经过A,B,C三点,点B的坐标为(-3,0),且OC=3OA,直线y=x+m经过B、C两点.
如图,已知抛物线y=ax2+bx+c(a≠0)经过A,B,C三点,点B的坐标为(-3,0),且OC=3OA,直线y=x+m经过B、C两点.