题目内容
11. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列判断正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列判断正确的是( )| A. | abc>0 | B. | a-b+c<0 | C. | b2-4ac<0 | D. | 2a+b=0 |
分析 结合抛物线的图象可知a>0,c<0;由抛物线交x轴的交点为(-3,0)、(1,0)可得出C答案不正确,且抛物线对称轴为x=-1,即a=b,即D答案不正确;结合a>0,c<0可得出abc<0,即A答案不正确;当x=-1时,函数的图象在x轴的下方可得出a-b+c<0,从而得出结论.
解答 解:∵抛物线开口向上,
∴a>0,
∵抛物线与y轴的交点在y轴的负半轴,
∴c<0,
∵抛物线的对称轴为x=-1,
∴-$\frac{b}{a}$=-1,即a=b>0.
A、∵a=b>0,c<0,∴abc<0,即A答案不正确;
B、当x=-1时,抛物线上的点在x下方,即y=a-b+c<0,即B答案正确;
C、∵抛物线与x轴有两个不同的交点,∴方程ax2+bx+c=0有两个不等实根,∴△=b2-4ac>0,即C答案不正确;
D、∵-$\frac{b}{a}$=-1,∴a=b,即D答案不正确.
故选B.
点评 本题考查了二次函数图象与系数的关系以及根的判别式,解题的关键结合图象判断各选项正确与否.本题属于基础题,难度不大,只要熟悉二次函数与图象的关系即可解决该类题目.

练习册系列答案
相关题目
 如图,直线l1∥l2,∠α=∠β,∠1=35°,则∠2=145°.
如图,直线l1∥l2,∠α=∠β,∠1=35°,则∠2=145°.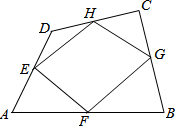 如图,E、F、G、H分别是凸四边形ABCD的四边的中点,顺次连接E、F、G、H这四点围成四边形EFGH.
如图,E、F、G、H分别是凸四边形ABCD的四边的中点,顺次连接E、F、G、H这四点围成四边形EFGH. 如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(20,0),(0,8),点D是OA的中点,点P在BC上运动,当△ODP是以10为腰长的等腰三角形时,点P的坐标为(6,8)或(4,8)或(16,8).
如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(20,0),(0,8),点D是OA的中点,点P在BC上运动,当△ODP是以10为腰长的等腰三角形时,点P的坐标为(6,8)或(4,8)或(16,8).