题目内容
1.在△ABC中,∠C=90°,AC=6,BC=8,点D是斜边AB上一点,当AD=$\frac{11}{5}$时,∠BDC=2∠B.分析 由勾股定理可求得AB的长,然后过点D作DF平分∠BDC交BC于F,过F作FG⊥AB于G,易得Rt△BFG∽Rt△BAC,然后由相似三角形的对应边成比例,求得CD的长,又由△CDF∽△CBD,求得答案.
解答 解:∵在△ABC中,∠C=90°,AC=6,BC=8,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10,
过点D作DF平分∠BDC交BC于F,过F作FG⊥AB于G,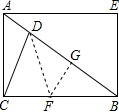 ∵∠BDC=2∠BAE=∠ABF,
∵∠BDC=2∠BAE=∠ABF,
∴∠FDB=∠FBD,
∴FD=FB,
∵∠BGF=∠ACB=90°,∠FBG=∠ABC,
∴Rt△BFG∽Rt△BAC,
∴FG:BG:BF=AC:BC:AB=3:4:5,
设FG=3x,则BG=4x,BF=5x,
∴DG=BG=4x,DF=BF=5x,
∴BD=2BG=8x,
∵∠CDF=$\frac{1}{2}$∠BDC=∠CBD,∠DCB为公共角,
∴△CDF∽△CBD,
∴CD:BC=DF:BD=5:8,
∴CD=$\frac{5}{8}$BC=5,
∵CD:CF=CB:CD,
∴CD2=CF•BC,
∴CF=$\frac{C{D}^{2}}{BC}$=$\frac{25}{8}$,
∴BF=8-$\frac{25}{8}$=$\frac{39}{8}$,
解得:x=$\frac{39}{40}$,
∴BD=8x=$\frac{39}{40}$.
∴AD=10-BD=$\frac{11}{5}$.
故答案为:$\frac{11}{5}$.
点评 此题考查了直角三角形的性质以及相似三角形的判定与性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.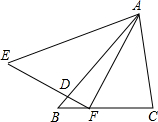 如图,在△ABC和△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.下列结论中正确的是( )
如图,在△ABC和△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.下列结论中正确的是( )
①∠AFC=∠C;②DF=CF;③△ADE∽△FDB;④∠BFD=∠CAF.
 如图,在△ABC和△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.下列结论中正确的是( )
如图,在△ABC和△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.下列结论中正确的是( )①∠AFC=∠C;②DF=CF;③△ADE∽△FDB;④∠BFD=∠CAF.
| A. | 只有①③ | B. | 只有①④ | C. | 只有③④ | D. | 只有①③④ |
10.已知a,b,c为△ABC的三条边,化简 $\sqrt{(a+b-c)^{2}}$-|b-a-c|=( )
| A. | b+c | B. | 0 | C. | b-c | D. | 2b-2c |
11. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列判断正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列判断正确的是( )
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列判断正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列判断正确的是( )| A. | abc>0 | B. | a-b+c<0 | C. | b2-4ac<0 | D. | 2a+b=0 |