题目内容
20．已知a，b，c是一个三角形的三条边长，则化简|a-b+c|-|b-a-c|=0．分析 根据三角形三边关系得到a-b+c＞0，b-a-c＜0，再去绝对值，合并同类项即可求解．
解答 解：∵a，b，c是一个三角形的三条边长，
∴a-b+c＞0，b-a-c＜0，
∴|a-b+c|-|b-a-c|
=a-b+c+b-a-c
=0．
故答案为：0．
点评 考查了三角形三边关系，绝对值的性质，整式的加减，关键是得到a-b+c＞0，b-a-c＜0．
练习册系列答案
相关题目
10．已知a，b，c为△ABC的三条边，化简 $\sqrt{（a+b-c）^{2}}$-|b-a-c|=（ ）
| A． | b+c | B． | 0 | C． | b-c | D． | 2b-2c |
11．
二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列判断正确的是（ ）
二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列判断正确的是（ ）| A． | abc＞0 | B． | a-b+c＜0 | C． | b2-4ac＜0 | D． | 2a+b=0 |
15．计算8的立方根与$\sqrt{81}$的平方根之和是（ ）
| A． | 5 | B． | 11 | C． | 5或-1 | D． | 11或-7 |
5．使分式$\frac{x-2012}{2x-8}$有意义的x的取值范围是（ ）
| A． | x=4 | B． | x≠4 | C． | x=-4 | D． | x≠-4 |
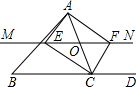如图，在△ABC中，O是AC上一动点（不与点A、C重合），过O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．