题目内容
3.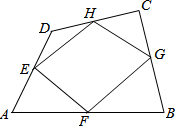 如图,E、F、G、H分别是凸四边形ABCD的四边的中点,顺次连接E、F、G、H这四点围成四边形EFGH.
如图,E、F、G、H分别是凸四边形ABCD的四边的中点,顺次连接E、F、G、H这四点围成四边形EFGH.(1)求证:四边形EFGH是平行四边形.
(2)要使四边形EFGH成为菱形,则AC与BD之间应满足的数量关系是AC=BD.
分析 (1)由三角形中位线定理得出HE∥AC,HE=$\frac{1}{2}$AC,GF∥AC,GF=$\frac{1}{2}$AC,因此HE=GF且HE∥GF;即可得出结论;
(2)由菱形的性质得出EF=HE,由(1)得:HE=$\frac{1}{2}$AC,同理:EF=$\frac{1}{2}$BD,因此AC=BC.
解答 (1)证明:如图1所示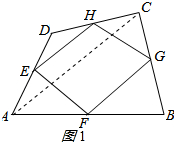 ,连接AC,
,连接AC,
∵E、F、G、H分别是四边形ABCD边的中点,
∴HE∥AC,HE=$\frac{1}{2}$AC,GF∥AC,GF=$\frac{1}{2}$AC,
∴HE=GF且HE∥GF;
∴四边形EFGH是平行四边形.
(2)解:连接BD,如图2所示:
若四边形EFGH成为菱形,
则EF=HE,
由(1)得:HE=$\frac{1}{2}$AC,
同理:EF=$\frac{1}{2}$BD,
∴AC=BC;
故答案为:AC=BD.
点评 本题考查了平行四边形的判定、中点四边形、菱形的性质、三角形中位线定理;熟练掌握三角形中位线定理是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下列说法正确的有( )
①不相交的两条直线是平行线;
②经过直线外一点,有且只有一条直线与这条直线平行;
③两条直线被第三条直线所截,同旁内角互补;
④在同一平面内,若直线a⊥b,b⊥c,则直线a与c不相交.
①不相交的两条直线是平行线;
②经过直线外一点,有且只有一条直线与这条直线平行;
③两条直线被第三条直线所截,同旁内角互补;
④在同一平面内,若直线a⊥b,b⊥c,则直线a与c不相交.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列判断正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列判断正确的是( )
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列判断正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列判断正确的是( )| A. | abc>0 | B. | a-b+c<0 | C. | b2-4ac<0 | D. | 2a+b=0 |
15.计算8的立方根与$\sqrt{81}$的平方根之和是( )
| A. | 5 | B. | 11 | C. | 5或-1 | D. | 11或-7 |
13.下列哪个点位于平面直角坐标系的第二象限( )
| A. | (2,3) | B. | (2,-3) | C. | (-2,3) | D. | (-2,-3) |