题目内容
15.已知:菱形有一个内角是120°,有一条对角线长是8cm,求菱形边长.分析 如图,根据题意得:∠ABC=120°,易得∠DAB=60°,所以△ABD为等边三角形.如果BD=8cm,那么AB=8cm;
如果AC=8cm,由菱形的性质可得边AB的长.
解答 
解:如上图,∵在菱形ABCD中,∠ADC=∠ABC=120°,
∴∠BAD=∠BCD=60°,
若BD=8cm,则AB=AC=BD=8cm,
若AC=8cm,AO=4cm,在Rt△ABO中,∠BAO=30°设OB=x,则AB=2x.由勾股定理得
x2+42=(2x)2,
解得 x=$\frac{4\sqrt{3}}{3}$cm
点评 此题考查了菱形的性质:菱形的边相等,对边平行,对角线互相平分且垂直还平分对角.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
3.若$\sqrt{{a}^{2}}$=($\sqrt{a}$)2,则a的取值范围是( )
| A. | a>0 | B. | a≥0 | C. | a=0 | D. | a<0 |
4.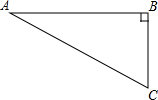 如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
 如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )| A. | $\frac{\sqrt{3}}{12}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
5.函数y=$\frac{2}{x+1}$的图象可能是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,在菱形ABCD中,E,F分别是AD,BD的中点,若EF=2,则菱形ABCD的周长是16.
如图,在菱形ABCD中,E,F分别是AD,BD的中点,若EF=2,则菱形ABCD的周长是16.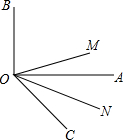 如图,ON平分∠AOC,OM平分∠BOC.
如图,ON平分∠AOC,OM平分∠BOC.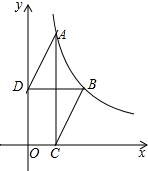 如图,函数y=$\frac{k}{x}(x>0)$的图象经过点A,B,点B的坐标为(1,1),过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,连接AD,BC.若AD∥BC,则线段BC的长度为$\frac{\sqrt{5}}{2}$.
如图,函数y=$\frac{k}{x}(x>0)$的图象经过点A,B,点B的坐标为(1,1),过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,连接AD,BC.若AD∥BC,则线段BC的长度为$\frac{\sqrt{5}}{2}$.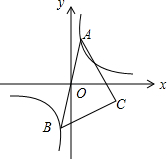 如图,已知点A是双曲线y=$\frac{4}{x}$在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-4.
如图,已知点A是双曲线y=$\frac{4}{x}$在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-4.