题目内容
1.计算:6$\sqrt{\frac{1}{3}}$-($\sqrt{3}$+1)2=-4.分析 首先化简二次根式,进而利用完全平方公式计算,求出答案.
解答 解:原式=6×$\frac{\sqrt{3}}{3}$-(3+2$\sqrt{3}$+1)
=2$\sqrt{3}$-4-2$\sqrt{3}$
=-4.
故答案为:-4.
点评 此题主要考查了二次根式的混合运算,正确掌握完全平方公式是解题关键.

练习册系列答案
相关题目
16.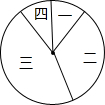 某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2,在第四组内的两名选手记为:B1、B2,从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果).
 某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:| 组号 | 分组 | 频数 |
| 一 | 6≤m<7 | 2 |
| 二 | 7≤m<8 | 7 |
| 三 | 8≤m<9 | a |
| 四 | 9≤m≤10 | 2 |
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2,在第四组内的两名选手记为:B1、B2,从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果).
6.下列命题为真命题的是( )
| A. | 有两边及一角对应相等的两个三角形全等 | |
| B. | 方程x2-x+2=0有两个不相等的实数根 | |
| C. | 面积之比为1:4的两个相似三角形的周长之比是1:4 | |
| D. | 顺次连接任意四边形各边中点得到的四边形是平行四边形 |
3.若$\sqrt{{a}^{2}}$=($\sqrt{a}$)2,则a的取值范围是( )
| A. | a>0 | B. | a≥0 | C. | a=0 | D. | a<0 |
4.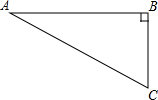 如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
 如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )| A. | $\frac{\sqrt{3}}{12}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
 如图,在菱形ABCD中,E,F分别是AD,BD的中点,若EF=2,则菱形ABCD的周长是16.
如图,在菱形ABCD中,E,F分别是AD,BD的中点,若EF=2,则菱形ABCD的周长是16.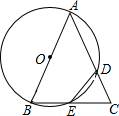 已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.