题目内容
7.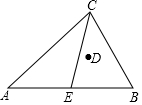 如图,AB=4,∠C=90°,E为AB中点,D为△ABC内心.当点C在AB上方运动时,则DE的最小值为2$\sqrt{2}$-2.
如图,AB=4,∠C=90°,E为AB中点,D为△ABC内心.当点C在AB上方运动时,则DE的最小值为2$\sqrt{2}$-2.
分析 连接DA、DB,根据内心的概念得到AD、BD是△ABC的角平分线,求出∠ADB=135°,根据圆周角定理、勾股定理计算即可.
解答 解: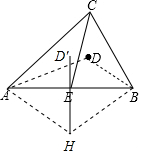 连接DA、DB,
连接DA、DB,
∵D为△ABC内心,
∴AD、BD是△ABC的角平分线,又∠C=90°,
∴∠ADB=135°,
∴点D在以AB为弦,∠ADB=135°的圆弧上,
设圆弧的圆心为H,连接HE并延长交圆弧于D′,
则当点C在AB上方运动时,D′E最小,
∵∠ADB=135°,
∴∠AHB=90°,
∴D′H=AH=2$\sqrt{2}$,EH=2,
∴D′E=2$\sqrt{2}$-2,
故答案为:2$\sqrt{2}$-2.
点评 本题考查的是三角形的内切圆和内心,掌握内心的性质、圆周角定理、等腰直角三角形的性质是解题的关键.

练习册系列答案
相关题目
18. 如图,经过原点O的⊙P与x、y轴分别交于A、B两点,点C是劣弧$\widehat{OB}$上一点,则∠ACB=( )
如图,经过原点O的⊙P与x、y轴分别交于A、B两点,点C是劣弧$\widehat{OB}$上一点,则∠ACB=( )
 如图,经过原点O的⊙P与x、y轴分别交于A、B两点,点C是劣弧$\widehat{OB}$上一点,则∠ACB=( )
如图,经过原点O的⊙P与x、y轴分别交于A、B两点,点C是劣弧$\widehat{OB}$上一点,则∠ACB=( )| A. | 80° | B. | 90° | C. | 100° | D. | 无法确定 |
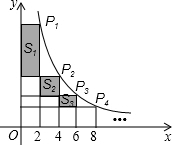 如图,在反比例函数y=$\frac{10}{x}$(x>0)的图象上,有点P1,P2,P3,P4,…,它们的横坐标依次为2,4,6,8,…分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次记为S1,S2,S3,…,Sn,则S1+S2+S3+…+Sn=10-$\frac{10}{n+1}$(用含n的代数式表示)
如图,在反比例函数y=$\frac{10}{x}$(x>0)的图象上,有点P1,P2,P3,P4,…,它们的横坐标依次为2,4,6,8,…分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次记为S1,S2,S3,…,Sn,则S1+S2+S3+…+Sn=10-$\frac{10}{n+1}$(用含n的代数式表示)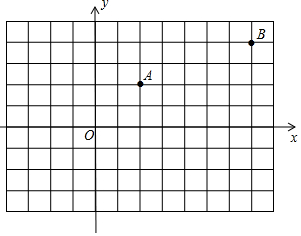 如图,已知A,B两村庄的坐标分别为(2,2),(7,4),一辆汽车从O点出发,在x轴上行驶.
如图,已知A,B两村庄的坐标分别为(2,2),(7,4),一辆汽车从O点出发,在x轴上行驶.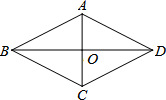 如图,菱形ABCD中,对角线AC、BD相交于点O.AC=3$\sqrt{2}$+2$\sqrt{3}$,BD=3$\sqrt{2}$-2$\sqrt{3}$.求:菱形ABCD的面积和周长.
如图,菱形ABCD中,对角线AC、BD相交于点O.AC=3$\sqrt{2}$+2$\sqrt{3}$,BD=3$\sqrt{2}$-2$\sqrt{3}$.求:菱形ABCD的面积和周长.