题目内容
16.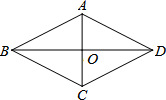 如图,菱形ABCD中,对角线AC、BD相交于点O.AC=3$\sqrt{2}$+2$\sqrt{3}$,BD=3$\sqrt{2}$-2$\sqrt{3}$.求:菱形ABCD的面积和周长.
如图,菱形ABCD中,对角线AC、BD相交于点O.AC=3$\sqrt{2}$+2$\sqrt{3}$,BD=3$\sqrt{2}$-2$\sqrt{3}$.求:菱形ABCD的面积和周长.
分析 根据菱形的对角线可以求得菱形ABCD的面积,根据菱形对角线互相垂直平分的性质,可以求得BO=OD,AO=OC,在Rt△AOD中,根据勾股定理可以求得AB的长,即可求菱形ABCD的周长.
解答 解:菱形的对角线为AC=3$\sqrt{2}$+2$\sqrt{3}$,BD=3$\sqrt{2}$-2$\sqrt{3}$.
则菱形的面积为$\frac{1}{2}$×(3$\sqrt{2}$+2$\sqrt{3}$)×(3$\sqrt{2}$-2$\sqrt{3}$)=3,
菱形对角线互相垂直平分,
∴BO=OD=$\frac{3\sqrt{2}-2\sqrt{3}}{2}$,AO=OC=$\frac{3\sqrt{2}+2\sqrt{3}}{2}$,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{15}$,
故菱形的周长为4$\sqrt{15}$,
答:菱形的周长为4$\sqrt{15}$,面积为3.
点评 本题考查了菱形面积的计算,考查了勾股定理在直角三角形中的运用,考查了菱形各边长相等的性质,本题中根据勾股定理计算AB的长是解题的关键.

练习册系列答案
相关题目
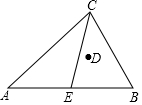 如图,AB=4,∠C=90°,E为AB中点,D为△ABC内心.当点C在AB上方运动时,则DE的最小值为2$\sqrt{2}$-2.
如图,AB=4,∠C=90°,E为AB中点,D为△ABC内心.当点C在AB上方运动时,则DE的最小值为2$\sqrt{2}$-2. 如图,∠B=62°,∠1=62°,∠D=36°.
如图,∠B=62°,∠1=62°,∠D=36°.