题目内容
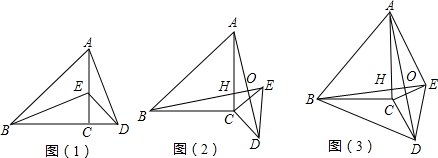
6.数学活动:图形的变化问题情境:如图(1),△ABC为等腰直角三角形,∠ACB=90°,E是AC边上的一个动点(点E与A,C不重合),以CE为边在△ABC外作等腰直角△ECD,∠ECD=90°,连接BE,AD.猜想线段BE,AD之间的关系.
(1)独立思考:请直接写出线段BE,AD之间的关系;
(2)合作交流:“希望”小组受上述问题的启发,将图(1)中的等腰直角△ECD绕着点C顺时针方向旋转至如图(2)的位置,BE交AC于点H,交AD于点O.(1)中的结论是否仍然成立,请说明理由.
(3)拓展延伸:“科技”小组将(2)中的等腰直角△ABC改为Rt△ABC,∠ACB=90°,AC=8,BC=6,将等腰直角△ECD改为Rt△ECD,∠ECD=90°,CD=4,CE=3.试猜想BD2+AE2是否为定值,结合图(3)说明理由.
分析 (1)由△ABC和△CDE都是等腰直角三角形,得到的结论,直接判断出△BCE≌△ACD,再用互余判断出垂直;
(2)由△ABC和△CDE都是等腰直角三角形,得到的结论,直接判断出△BCE≌△ACD,再用互余判断出垂直;
(3)由条件用两边对应成比例,夹角相等判断出△BCE∽△ACD,再用勾股定理简单的计算即可.
解答 解:(1)∵△ABC和△CDE都是等腰直角三角形,
∴BC=AC,CE=CD,∠BCE=∠ACD=90°,
∴△BCE≌△ACD,
∴BE=AD,∠CEB=∠CDA,
∵∠CBE+∠CEB=90°,
∴∠CBE+∠CDA=90°,
∴BE⊥AD,
(2)BE=CD,BE⊥AD,
理由:∵△ABC是等腰直角三角形,∠ACB=90°
∴AC=BC,
∵△CDE是等腰直角三角形,∠ECD=90°,
∴CD=CE,
∴∠ACB+∠ACE=∠ECD+∠ACE,
∴∠BCE=∠ACD,
∴△BCE≌△ACD,
∴BE=AD,∠CBE=∠CAD,
∵∠BHC=∠AHO,∠CBH+∠BHC=90°,
∴∠CAD+∠AHO=90°,
∴∠AHO=90°,
∴BE⊥AD;
即:BE=AD,BE⊥AD;
(3)是定值,
理由:∵∠ECD=90°,∠ACB=90°,
∴∠ACB=∠ECD,
∴∠ACB+ACE=∠ECD+∠ACE=90°,
∴∠BCE=ACD,
∵AC=8,BC=6,CD=4,CE=3,
∴$\frac{BC}{AC}=\frac{CE}{CD}$=$\frac{3}{4}$,
∴△BCE∽△ACD,
∴∠CBE=∠CAD,
∵∠BHC=∠AHO,∠CBH+∠BHC=90°,
∴∠CAD+∠AHO=90°,
∴∠AOH=90°,
∴BE⊥AD,
∴∠BOD=∠AOB=90°,
∴BD2=OB2+OD2,AE2=OA2+OE2,AB2=OA2+OB2,DE2=OE2+OD2,
∴BD2+AE2=OB2+OD2+OA2+OE2=AB2+DE2,
在Rt△ABC中,∠ACB=90°,AC=8,BC=6,
∴AB2=100,
在Rt△ECD中,∠ECD=90°,CD=4,CE=3,
∴DE2=25,
∴BD2+AE2=AB2+DE2=125.
点评 此题是几何变换综合题,主要考查了全等三角形的性质和判定,相似三角形的判定和性质,勾股定理,解本题的关键是判断三角形全等和相似,难点是用勾股定理的 计算定值.

| A. |  | B. |  | C. |  | D. |  |
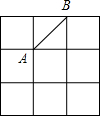 在边长为2的小正方形组成的网格中,有如图所示的A,B两点,在格点上任意放置点C,恰好能使得△ABC的面积为2的概率为( )
在边长为2的小正方形组成的网格中,有如图所示的A,B两点,在格点上任意放置点C,恰好能使得△ABC的面积为2的概率为( )| A. | $\frac{3}{16}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{5}{16}$ |
