题目内容
2.下面是某同学在一次测试中解答的填空题:①x2=a2,则x=a;②方程2x(x-2)=x-2的解为x=0;③已知x1,x2是方程2x2+3x-4=0的两根,则x1+x2=$\frac{3}{2}$,x1x2=-2.其中错误答案的序号是①②③.分析 ①两个数的平方相等,则可能相等也可能互为相反数,所以不正确;
②一元二次方程应该有两个根,而题中只有一个,所以不对;
③根据根与系数的关系解答即可判断.
解答 解:①若x2=a2,则x=±a,故错误;
②方程2x(x-2)=x-2
即(x-2)(2x-1)=0,解为x1=2,x2=$\frac{1}{2}$,故错误;
③已知x1,x2是方程2x2+3x-4=0的两根,则x1+x2=-$\frac{3}{2}$,x1x2=-2.故错误;
其中错误答案的序号是①②③,
故答案为:①②③.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了分式的值为零的条件.

练习册系列答案
相关题目
 在长为10m,宽为8m的矩形空地上,沿平行于矩形各边的方向分割出三个全等的小矩形花圃,要使小矩形花圃的面积和为24m2,示意图如图所示,求其中一个小矩形花圃的长和宽.
在长为10m,宽为8m的矩形空地上,沿平行于矩形各边的方向分割出三个全等的小矩形花圃,要使小矩形花圃的面积和为24m2,示意图如图所示,求其中一个小矩形花圃的长和宽.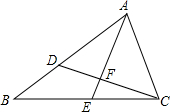 如图,已知AD=2,DB=1,∠ACD=∠B,∠BAC的平分线分别交CD,BC于F,求$\frac{AF}{AE}$的值.
如图,已知AD=2,DB=1,∠ACD=∠B,∠BAC的平分线分别交CD,BC于F,求$\frac{AF}{AE}$的值.