题目内容
7．若$\frac{a+1}{2}=\frac{b+2}{3}=\frac{c+3}{4}$，且2a+3b+4c=38，求a，b，c．分析 根据比例的性质，可得b=$\frac{3a-1}{2}$，c=2a+1，根据解方程，可得答案．
解答 解：由$\frac{a+1}{2}=\frac{b+2}{3}=\frac{c+3}{4}$，得
b=$\frac{3a-1}{2}$，c=2a+1．
将b=$\frac{3a-1}{2}$，c=2a+1代入2a+3b+4c=38，得
2a+$\frac{9a-3}{2}$+8a+4=38，
解得a=$\frac{71}{29}$，b=$\frac{3×\frac{71}{29}-1}{2}$=$\frac{97}{29}$，c=2×$\frac{71}{29}$+1=$\frac{171}{29}$．
点评 本题考查了比例的性质，利用比例的性质得出b=$\frac{3a-1}{2}$，c=2a+1是解题关键．
练习册系列答案
相关题目
如图所示，已知在△ABC中，∠C=90°，BD平分∠ABC，若AC=21cm，且CD：AD=3：4，求点D到AB的距离．
如图，在Rt△ABC中，∠ACB=90°，∠A=30°，CD⊥AB，DE⊥BD，D，E分别为垂足，F为AB的中点，若以点D为圆心，$\frac{1}{2}$CD为半径画⊙D，试判定B，E，F与⊙D的位置关系．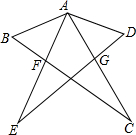
如图，AC=AE，∠C=∠E，∠BAC=∠DAE．求证：