题目内容
15.有一种用“☆”定义的新运算:对于任意实数a,b都有a☆b=b2+a.例如7☆4=42+7=23.(1)已知m☆2的结果是6,则m的值是多少?
(2)将两个实数n和n+2用这种新定义“☆”加以运算,结果为4,则n的值是多少?
分析 (1)已知代数式利用题中新定义化简列出方程,求出方程的解即可得到m的值;
(2)利用新定义列出方程,求出方程的解即可得到n的值.
解答 解:(1)根据题中的新定义得:m☆2=4+m=6,
解得:m=2;
(2)根据题意得:n☆(n+2)=4,即(n+2)2+n=4,
解得:n=0或n=-5;
(n+2)☆n=n2+n+2=4,
解得:n=-2或n=1,
则n=0或-5或-2或1.
点评 此题考查了实数的运算,弄清题中的新定义是解本题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
5.如果-3a2ybx+1与$\frac{1}{5}$a3xby是同类项,则( )
| A. | $\left\{\begin{array}{l}{x=-2}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-2}\\{y=-3}\end{array}\right.$ |
3.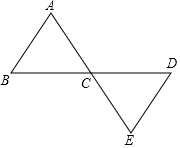 如图,连接在一起的两个等边三角形的边长都为2cm,一个微型机器人由点A开始按A→B→C→D→E→C→A→B→C…的顺序沿等边三角形的边循环移动. 当微型机器人移动了2016cm后,它停在了点A上.
如图,连接在一起的两个等边三角形的边长都为2cm,一个微型机器人由点A开始按A→B→C→D→E→C→A→B→C…的顺序沿等边三角形的边循环移动. 当微型机器人移动了2016cm后,它停在了点A上.
 如图,连接在一起的两个等边三角形的边长都为2cm,一个微型机器人由点A开始按A→B→C→D→E→C→A→B→C…的顺序沿等边三角形的边循环移动. 当微型机器人移动了2016cm后,它停在了点A上.
如图,连接在一起的两个等边三角形的边长都为2cm,一个微型机器人由点A开始按A→B→C→D→E→C→A→B→C…的顺序沿等边三角形的边循环移动. 当微型机器人移动了2016cm后,它停在了点A上.  如图,若要用“HL”证明Rt△ABC≌Rt△ABD,则需要添加的一个条件是AC=AD或BC=BD.
如图,若要用“HL”证明Rt△ABC≌Rt△ABD,则需要添加的一个条件是AC=AD或BC=BD.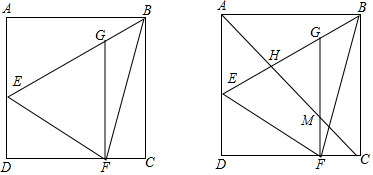
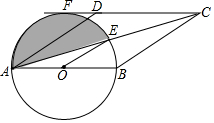 四边形ABCD的对角线交于点E,有AE=EC,BE=ED,以AB为直径的⊙O过点E.
四边形ABCD的对角线交于点E,有AE=EC,BE=ED,以AB为直径的⊙O过点E. +(a-3b)2=2a2+5b2
+(a-3b)2=2a2+5b2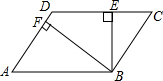 如图,?ABCD中,BE⊥CD,BF⊥AD,垂足分别为E、F,CE=3,DF=4,∠EBF=60°,求?ABCD的面积.
如图,?ABCD中,BE⊥CD,BF⊥AD,垂足分别为E、F,CE=3,DF=4,∠EBF=60°,求?ABCD的面积.