题目内容
5.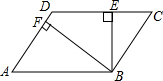 如图,?ABCD中,BE⊥CD,BF⊥AD,垂足分别为E、F,CE=3,DF=4,∠EBF=60°,求?ABCD的面积.
如图,?ABCD中,BE⊥CD,BF⊥AD,垂足分别为E、F,CE=3,DF=4,∠EBF=60°,求?ABCD的面积.
分析 求出∠D=120°,根据平行四边形的性质求出∠A=∠C=60°,解直角三角形求出BC=AD=6,求出AF,解直角三角形求出BF,求出面积即可.
解答 解:∵BE⊥CD,BF⊥AD,
∴∠BEC=90°,∠BED=∠BFD=90°,
∵∠EBF=60°,
∴∠D=120°,
∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠C=180°-∠D=60°,
∴∠A=∠C=60°,
∵CE=3,
∴BC=2CE=6,
∴AD=BC=6,
∵DF=4,
∴AF=2,
∴AB=2AF=4,BF=2$\sqrt{3}$,
∴?ABCD的面积是AD×BF=6×2$\sqrt{3}$=12$\sqrt{3}$.
点评 本题考查了平行四边形的性质,解直角三角形的应用,注意:平行四边形的对边平行且相等,平行四边形的面积等于底乘以高.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
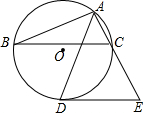 如图,△ABC内接于⊙O,AD平分∠BAC交⊙O于点D,过点D作DE∥BC交AC的延长线于点E.
如图,△ABC内接于⊙O,AD平分∠BAC交⊙O于点D,过点D作DE∥BC交AC的延长线于点E.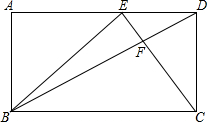 如图所示,长方形ABCD中,点E为AD边上的一点,连接BD,CE相交于点F,三角形EFD、三角形DFC的面积分别10,25平方厘米.
如图所示,长方形ABCD中,点E为AD边上的一点,连接BD,CE相交于点F,三角形EFD、三角形DFC的面积分别10,25平方厘米.