题目内容
15.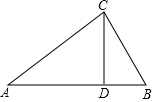 某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=80m,BC=60m.线段CD是一条水渠,且D点在边AB上,已知水渠的造价为1000元/m,问:当水渠的造价最低时,CD长为多少米?最低造价是多少元?
某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=80m,BC=60m.线段CD是一条水渠,且D点在边AB上,已知水渠的造价为1000元/m,问:当水渠的造价最低时,CD长为多少米?最低造价是多少元?
分析 当CD为斜边上的高时,CD最短,从而水渠造价最低,根据已知条件可将CD的长求出,在Rt△ACD中运用勾股定理可将AD边求出.
解答 解:当CD为斜边上的高时,CD最短,从而水渠造价最低,
∵∠ACB=90°,AC=80米,BC=60米,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}=\sqrt{6{0}^{2}+8{0}^{2}}$=100米,
∵CD•AB=AC•BC,即CD•100=80×60,
∴CD=48米,
∴在Rt△ACD中,AC=80,CD=48,
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}=\sqrt{8{0}^{2}-4{8}^{2}}$=64米,
所以,CD长为48米,水渠的造价最低,其最低造价为48000元.
点评 此题考查勾股定理的应用,本题的关键是确定D点的位置,在运算过程中多次用到勾股定理.

练习册系列答案
相关题目
3.下列函数中是二次函数的是( )
| A. | y=3x-1 | B. | y=x3-2x-3 | C. | y=(x+1)2-x2 | D. | y=3x2-1 |

 BF和BE分别是∠ABC和∠ABD的角平分线,点D、B、C在同一直线上,AE⊥BE于点E,AF⊥BF于点F,试证明AB=EF.
BF和BE分别是∠ABC和∠ABD的角平分线,点D、B、C在同一直线上,AE⊥BE于点E,AF⊥BF于点F,试证明AB=EF. 用四个全等的直角三角形拼成了一个如图所示的图形,其中a表示较短直角边,b表示较长的直角边,c表示斜边,你能用这个图形证明勾股定理吗?
用四个全等的直角三角形拼成了一个如图所示的图形,其中a表示较短直角边,b表示较长的直角边,c表示斜边,你能用这个图形证明勾股定理吗?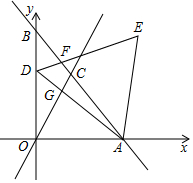 如图,已知一次函数y=-$\sqrt{3}$x+2$\sqrt{3}$的图象与x轴、y轴分别交于A、B两点,与正比例函数y=$\sqrt{3}$x的图象交于点C,点D是线段OB上的一个动点(不包含O、B两点),以AD为边在其一侧作等边三角形ADE,DE交AB于F,AD交OC于G.
如图,已知一次函数y=-$\sqrt{3}$x+2$\sqrt{3}$的图象与x轴、y轴分别交于A、B两点,与正比例函数y=$\sqrt{3}$x的图象交于点C,点D是线段OB上的一个动点(不包含O、B两点),以AD为边在其一侧作等边三角形ADE,DE交AB于F,AD交OC于G.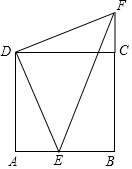 已知:如图,E点是正方形ABCD的边AB上一点,AB=4,DE=6,△DAE逆时针旋转后能够与△DCF重合.
已知:如图,E点是正方形ABCD的边AB上一点,AB=4,DE=6,△DAE逆时针旋转后能够与△DCF重合.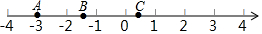 如图所示,数轴上有A、B、C三个点,且点B是线段AC的中点,点A表示-3,点B表示的是-$\sqrt{2}$,则点C表示的数是-2$\sqrt{2}$+3.
如图所示,数轴上有A、B、C三个点,且点B是线段AC的中点,点A表示-3,点B表示的是-$\sqrt{2}$,则点C表示的数是-2$\sqrt{2}$+3.