题目内容
20.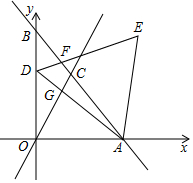 如图,已知一次函数y=-$\sqrt{3}$x+2$\sqrt{3}$的图象与x轴、y轴分别交于A、B两点,与正比例函数y=$\sqrt{3}$x的图象交于点C,点D是线段OB上的一个动点(不包含O、B两点),以AD为边在其一侧作等边三角形ADE,DE交AB于F,AD交OC于G.
如图,已知一次函数y=-$\sqrt{3}$x+2$\sqrt{3}$的图象与x轴、y轴分别交于A、B两点,与正比例函数y=$\sqrt{3}$x的图象交于点C,点D是线段OB上的一个动点(不包含O、B两点),以AD为边在其一侧作等边三角形ADE,DE交AB于F,AD交OC于G.(1)分别求出A、B、C点的坐标;
(2)求证:△ADF和△ACG是否相似,为什么?
(3)证明CE总与AB垂直.
分析 (1)对于一次函数y=-$\sqrt{3}$x+2$\sqrt{3}$,令x=0,得y=2$\sqrt{3}$,令y=0得x=2,即可求出A、B两点坐标,由$\left\{\begin{array}{l}{y=-\sqrt{3}x+2\sqrt{3}}\\{y=\sqrt{3}x}\end{array}\right.$解方程组即可求得点C坐标.
(2)只要证明△AOC是等边三角形,可得∠ACG=∠ADF=60°,由此即可证明.
(3)连接EC,只要证明△OAD≌△CAE,可得∠AOD=∠ACE=90°,由此即可证明.
解答 (1)解:对于一次函数y=-$\sqrt{3}$x+2$\sqrt{3}$,令x=0,得y=2$\sqrt{3}$,
令y=0得x=2,
∴A(2,0),B(0,2$\sqrt{3}$),
由$\left\{\begin{array}{l}{y=-\sqrt{3}x+2\sqrt{3}}\\{y=\sqrt{3}x}\end{array}\right.$解得$\left\{\begin{array}{l}{x=1}\\{y=\sqrt{3}}\end{array}\right.$,
∴点C坐标为(1,$\sqrt{3}$).
(2)解:结论:△ADF∽△ACG.
理由:∵C(1,$\sqrt{3}$),A(2,0),
∴OC=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2,AC=$\sqrt{(2-1)^{2}+(\sqrt{3})^{2}}$=2,
∴OC=AC=OA,
∴△AOC是等边三角形,
∴∠ACG=60°,
∵△ADE是等边三角形,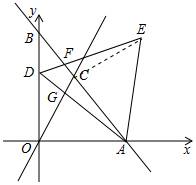
∴∠ADE=60°,
∴∠ACG=∠ADF,∵∠CAG=∠DAF,
∴△ADF∽△ACG.
(3)证明:连接EC,
∵△AOC,△ADE都是等边三角形,
∴AO=AC,AD=AE,∠OAC=∠DAE,
∴∠OAD=∠CAE,
在△OAD和△CAE中,
$\left\{\begin{array}{l}{OA=AC}\\{∠OAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△OAD≌△CAE(ASA),
∴∠AOD=∠ACE=90°,
∴EC⊥AB.
点评 本题考查相似三角形综合题、一次函数的应用、全等三角形的判定和性质、等边三角形的判定和性质等知识,解题的关键是熟练掌握待定系数法,学会利用方程组求两个函数的交点坐标,本题的突破点是证明△AOC是等边三角形.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案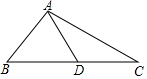 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长是( )
如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长是( )| A. | 3$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{2}$ |
| A. | 1 | B. | -1 | C. | 11 | D. | -11 |
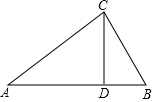 某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=80m,BC=60m.线段CD是一条水渠,且D点在边AB上,已知水渠的造价为1000元/m,问:当水渠的造价最低时,CD长为多少米?最低造价是多少元?
某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=80m,BC=60m.线段CD是一条水渠,且D点在边AB上,已知水渠的造价为1000元/m,问:当水渠的造价最低时,CD长为多少米?最低造价是多少元?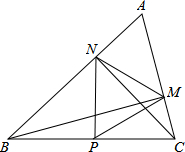 如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM.PN.
如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM.PN.