题目内容
5.按要求完成下列画图.(不写作法,保留作图痕迹,并分别写出结论)
(1)如图1,在△ABC中,∠BAC是钝角,
①用尺规作∠BAC的角平分线AE.
②用三角板作AC边上的高BD.
③用尺规作AB边上的垂直平分线MN.
(2)如图2,以格点为顶点分别按下列要求画三角形:
④在图①中,画一个三角形,使它的边长都是有理数
⑤在图②中画一个直角三角形,使它的边长都是无理数.
分析 (1)根据角平分线、垂线及中垂线的基本作图可得;
(2)作AC=4、BC=3、AB=5的△ABC和DF=$\sqrt{2}$、EF=2$\sqrt{2}$、DE=$\sqrt{10}$的Rt△DEF可得.
解答 解:(1)如图1,①AE即为所求;
②BD即为所求;
③直线MN即为所求;
(2)④如图2,△ABC即为所求;
⑤Rt△DEF即为所求.
点评 本题主要考查角平分线、垂线及中垂线的基本作图和勾股定理的运用,要熟悉三角形的高、中线、角平分线的定义,还要熟悉角平分线、高、中线的作法,特别注意,钝角三角形钝角边上的高在钝角边的延长线上.

练习册系列答案
相关题目
10.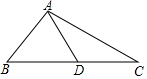 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长是( )
如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长是( )
 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长是( )
如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长是( )| A. | 3$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{2}$ |
14.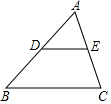 如图,DE∥BC,在下列比例式中,不能成立的是( )
如图,DE∥BC,在下列比例式中,不能成立的是( )
 如图,DE∥BC,在下列比例式中,不能成立的是( )
如图,DE∥BC,在下列比例式中,不能成立的是( )| A. | $\frac{AB}{AD}$=$\frac{AC}{AE}$ | B. | $\frac{AD}{DB}$=$\frac{AE}{EC}$ | C. | $\frac{AD}{DB}$=$\frac{DE}{BC}$ | D. | $\frac{AD}{DE}$=$\frac{AB}{BC}$ |
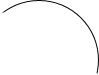 如图为一段圆弧形弯道,弯道长12π米,圆弧所对的圆心角是81°.
如图为一段圆弧形弯道,弯道长12π米,圆弧所对的圆心角是81°.
 已知:AB⊥BD于点B,DE⊥BD于点D,且CD=BA,DE=BC,求证:AC=CE,AC⊥CE.
已知:AB⊥BD于点B,DE⊥BD于点D,且CD=BA,DE=BC,求证:AC=CE,AC⊥CE. 如图,已知一次函数y=-$\frac{3}{4}$x+3的图象与x轴和y轴分别相交于A,B两点,点C在AB上,以1个单位/s的速度从点B向A运动,同时点D在线段AO上以同样的速度从点A向O运动,运动时间用t(s)表示.
如图,已知一次函数y=-$\frac{3}{4}$x+3的图象与x轴和y轴分别相交于A,B两点,点C在AB上,以1个单位/s的速度从点B向A运动,同时点D在线段AO上以同样的速度从点A向O运动,运动时间用t(s)表示.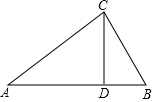 某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=80m,BC=60m.线段CD是一条水渠,且D点在边AB上,已知水渠的造价为1000元/m,问:当水渠的造价最低时,CD长为多少米?最低造价是多少元?
某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=80m,BC=60m.线段CD是一条水渠,且D点在边AB上,已知水渠的造价为1000元/m,问:当水渠的造价最低时,CD长为多少米?最低造价是多少元?