题目内容
20. 如图,在四边形ABCD中,∠DAB=60°,∠BCD=150°,对角线AC平分∠DAB,AC=6,则△DAB的面积为9$\sqrt{3}$.
如图,在四边形ABCD中,∠DAB=60°,∠BCD=150°,对角线AC平分∠DAB,AC=6,则△DAB的面积为9$\sqrt{3}$.
分析 作高线DF,根据∠DAF=60°,设AF=x,则AD=2x,DF=$\sqrt{3}$x,证明△ADC∽△ACB,则$\frac{AD}{AC}=\frac{AC}{AB}$,得
AD•AB=AC2=62=36,整体代入面积公式可得结论.
解答 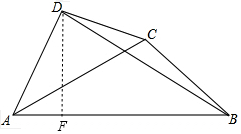 解:∵AC平分∠DAB,∠DAB=60°,
解:∵AC平分∠DAB,∠DAB=60°,
∴∠DAC=∠BAC=30°,
∴∠ADC+∠ACD=150°,
∵∠DCB=150°,
∴∠ACB+∠ACD=150°,
∴∠ADC=∠ACB,
∴△ADC∽△ACB,
∴$\frac{AD}{AC}=\frac{AC}{AB}$,
∴AD•AB=AC2=62=36,
过D作DF⊥AB于F,
在Rt△ADF中,∠DAF=60°,
∴∠ADF=30°,
设AF=x,则AD=2x,DF=$\sqrt{3}$x,
∴S△ABD=$\frac{1}{2}$AB•DF=$\frac{1}{2}$AB$•\sqrt{3}$x=$\frac{\sqrt{3}}{2}$AB•2x$•\frac{1}{2}$=$\frac{\sqrt{3}}{4}$AB•AD=$\frac{\sqrt{3}}{4}$×36=9$\sqrt{3}$;
故答案为:9$\sqrt{3}$.
点评 本题考查了相似三角形的性质和判定、角平分线的定义、直角三角形30°角的性质,本题证明△ADC∽△ACB是关键,还运用了整体的思想,使问题得以解决.

练习册系列答案
相关题目
12.在下列各组数中,是勾股数的一组是( )
| A. | 0.3,0.4,0.5 | B. | 4,5,6 | C. | $\frac{3}{5}$,$\frac{4}{5}$,1 | D. | 24,45,51 |
9.下列二次根式中属于最简二次根式的是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{0.3}$ | C. | $\sqrt{\frac{1}{3}}$ | D. | $\sqrt{3}$ |

 如图,在矩形ABCD中,AB=6,BC=8,G为AD中点,若E为AB边上一动点,当△CGE的周长为最小值时,则AE的长为2.
如图,在矩形ABCD中,AB=6,BC=8,G为AD中点,若E为AB边上一动点,当△CGE的周长为最小值时,则AE的长为2.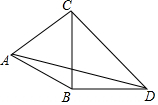 如图,△ABC是等边三角形,∠CBD=90°,BD=DC,则∠BAD的度数是15°.
如图,△ABC是等边三角形,∠CBD=90°,BD=DC,则∠BAD的度数是15°.
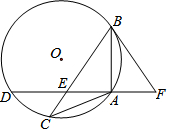 如图,△ABC内接于⊙O,AB=AC,过点A作AD⊥AB交⊙O于点D,交BC于点E,点F在DA的延长线上,且∠ABF=∠C.
如图,△ABC内接于⊙O,AB=AC,过点A作AD⊥AB交⊙O于点D,交BC于点E,点F在DA的延长线上,且∠ABF=∠C.