题目内容
19.令a、b、c三个数中最大数记作max{a,b,c},直线y=$\frac{1}{2}$x+t与函数y=max{-x2+4,x-2,-x-2}的图象有且只有3个公共点,则t的值为1或$\frac{65}{16}$.分析 只需画出函数y=max{-x2+4,x-2,-x-2}的图象,然后结合图象并运用分类讨论的思想,就可解决问题.
解答 解:在直角坐标系中画出函数y=max{-x2+4,x-2,-x-2}的图象,如图所示.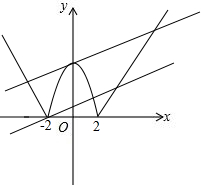
当直线y=$\frac{1}{2}$x+t经过(-2,0)或与抛物线y=-x2+4相切时,
直线y=$\frac{1}{2}$x+t与函数y=max{-x2+4,x-2,-x-2}的图象有且只有3个公共点.
①若直线y=$\frac{1}{2}$x+t经过(-2,0),
则有0=$\frac{1}{2}$×(-2)+t,
解得t=1;
②若直线y=$\frac{1}{2}$x+t与抛物线y=-x2+4相切,
则关于x的方程$\frac{1}{2}$x+t=-x2+4即x2+$\frac{1}{2}$x+t-4=0有两个相等的实数根,
则△=($\frac{1}{2}$)2-4×1×(t-4)=0,
解得t=$\frac{65}{16}$.
综上所述:t=1或$\frac{65}{16}$.
故答案为1或$\frac{65}{16}$.
点评 本题属于新定义型,主要考查了直线与抛物线的交点、根的判别式、直线上点的坐标特征等知识,在解决问题的个过程中用到了数形结合和分类讨论的数学思想,应熟练掌握.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
10.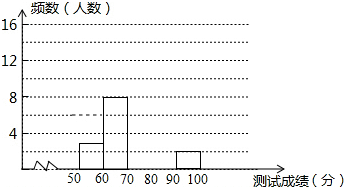 为了增强学生法律意识,某校举办了首届“法律进校园,法在我心中”知识大赛,经选拔后有25名学生参加决赛,这25名学生同时解答50个选择题,若每正确一个选择题得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
为了增强学生法律意识,某校举办了首届“法律进校园,法在我心中”知识大赛,经选拔后有25名学生参加决赛,这25名学生同时解答50个选择题,若每正确一个选择题得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
(1)求表中m的值;
(2)请把频数分布直方图补充完整;
(3)第4组的同学将抽出2名对第一组2名同学进行“一帮一”辅导,则第4组的小王与小李能同时抽到的概率是多少?
 为了增强学生法律意识,某校举办了首届“法律进校园,法在我心中”知识大赛,经选拔后有25名学生参加决赛,这25名学生同时解答50个选择题,若每正确一个选择题得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
为了增强学生法律意识,某校举办了首届“法律进校园,法在我心中”知识大赛,经选拔后有25名学生参加决赛,这25名学生同时解答50个选择题,若每正确一个选择题得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 3 |
| 第2组 | 60≤x<70 | 7 |
| 第3组 | 70≤x<80 | 10 |
| 第4组 | 80≤x<90 | m |
| 第5组 | 90≤x<100 | 2 |
(2)请把频数分布直方图补充完整;
(3)第4组的同学将抽出2名对第一组2名同学进行“一帮一”辅导,则第4组的小王与小李能同时抽到的概率是多少?
4.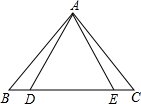 如图,已知△ABE≌△ACD,下列不正确的等式是( )
如图,已知△ABE≌△ACD,下列不正确的等式是( )
 如图,已知△ABE≌△ACD,下列不正确的等式是( )
如图,已知△ABE≌△ACD,下列不正确的等式是( )| A. | AB=AC | B. | ∠BAE=∠CAD | C. | BE=DC | D. | AD=DE |
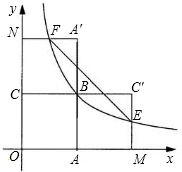 如图,四边形OABC是面积为4的正方形,函数$y=\frac{k}{x}$(x>0)的图象经过点B.
如图,四边形OABC是面积为4的正方形,函数$y=\frac{k}{x}$(x>0)的图象经过点B.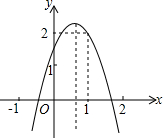 如图,已知二次函数y=ax2+bx+c(a≠0)的图形经过点(1,2),且与x轴交点的横坐标分别为x1,x2,其中-1<x1<0,1<x2<2,下列结论:①abc<0;②a<b<-2a;③b2+8a<4ac;④-1<a<0.其中正确结论的序号是①②.
如图,已知二次函数y=ax2+bx+c(a≠0)的图形经过点(1,2),且与x轴交点的横坐标分别为x1,x2,其中-1<x1<0,1<x2<2,下列结论:①abc<0;②a<b<-2a;③b2+8a<4ac;④-1<a<0.其中正确结论的序号是①②. 如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段DE,点A、B、D、E均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段DE,点A、B、D、E均在小正方形的顶点上.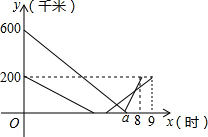 甲、乙两车在连通A、B、C三地的公路上行驶,B地在A地、C地之间,甲车从A地出发匀速向C地行驶,同时乙车从C地出发匀速向B地行驶,到达B地并在B地停留1h后,按原路原速返回到C地.在两车行驶的过程中,甲、乙两车距B地的路程y(km)与行驶时间x(h)之间的函数图象如图所示.下列说法:
甲、乙两车在连通A、B、C三地的公路上行驶,B地在A地、C地之间,甲车从A地出发匀速向C地行驶,同时乙车从C地出发匀速向B地行驶,到达B地并在B地停留1h后,按原路原速返回到C地.在两车行驶的过程中,甲、乙两车距B地的路程y(km)与行驶时间x(h)之间的函数图象如图所示.下列说法: