题目内容
11．解不等式组$\left\{\begin{array}{l}{5x＜1+4x}\\{\frac{1-x}{2}≤\frac{x+4}{3}}\end{array}\right.$，并在数轴上表示不等式组的解集．分析 分别求出各不等式的解集，再求出其公共解集，并在数轴上表示出来即可．
解答 解：$\left\{\begin{array}{l}{5x＜1+4x①}\\{\frac{1-x}{2}≤\frac{x+4}{3}②}\end{array}\right.$，
由①得，x＜1，
由②得x≥-1，
故此不等式组的解集为-1≤x＜1，
在数轴上表示为：
点评 本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
相关题目
如图，在钝角△ABC中，点D是BC的中点，分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF，M、N分别为AB、AC的中点，连接DM、DN、DE、DF、EM、EF、FN．求证：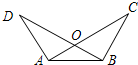
如图，已知∠D=∠C，还需添加一个条件是∠ABD=∠BAC或∠ABC=∠BAD，使得△ABD≌△BAC，依据是AAS或ASA．
把线段AB先向右平移2个单位长度，再向上平移3个单位长度，得到线段CD，请画出线段CD，并写出C，D两点的坐标．
20．
如图，在平行四边形ABCD中，E是CD延长线上一点，BE与AD交于F，若CD=2DE，则$\frac{{S}_{△DEF}}{{S}_{△ABF}}$等于（ ）
如图，在平行四边形ABCD中，E是CD延长线上一点，BE与AD交于F，若CD=2DE，则$\frac{{S}_{△DEF}}{{S}_{△ABF}}$等于（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{8}$ |