题目内容
7.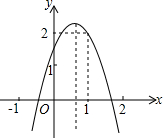 如图,已知二次函数y=ax2+bx+c(a≠0)的图形经过点(1,2),且与x轴交点的横坐标分别为x1,x2,其中-1<x1<0,1<x2<2,下列结论:①abc<0;②a<b<-2a;③b2+8a<4ac;④-1<a<0.其中正确结论的序号是①②.
如图,已知二次函数y=ax2+bx+c(a≠0)的图形经过点(1,2),且与x轴交点的横坐标分别为x1,x2,其中-1<x1<0,1<x2<2,下列结论:①abc<0;②a<b<-2a;③b2+8a<4ac;④-1<a<0.其中正确结论的序号是①②.
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,根据对称轴在y轴的右侧,a,b异号,b>0,判断①;根据对称轴小于1,判断②;根据顶点的纵坐标大于2判断③,根据图象经过(1,2)判断④.
解答 解:∵抛物线的开口向下,∴a<0,
∵抛物线与y轴的正半轴相交,∴c>0,
∵对称轴在y轴的右侧,a,b异号,∴b>0,
∴①abc<0,正确;
∵-$\frac{b}{2a}$<1,
∴b<-2a,
∴②a<b<-2a正确;
由于抛物线的顶点纵坐标大于2,即:$\frac{4ac-{b}^{2}}{4a}$>2,
由于a<0,所以4ac-b2<8a,即b2+8a>4ac,故③错误,
由题意知,a+b+c=2,(1)
a-b+c<0,(2)
4a+2b+c<0,(3)
把(1)代入(3)得到:4a+b+2-a<0,
则a<$\frac{-b-2}{3}$.
由(1)代入(2)得到:b>1.
则a<-1.故④错误.
综上所述,正确的结论是①②.
故答案为①②.
点评 本题考查了图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
17.若a满足|2015-a|+$\sqrt{a-2016}$=a,则20152-a的值为( )
| A. | 2015 | B. | -2015 | C. | 2016 | D. | -2016 |
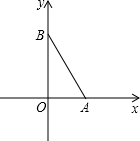 如图,△OAB中,∠AOB=90°,AO=1,BO=2.以AO为x轴,BO为y轴建立平面直角坐标系,O为原点.二次函数y=x2+bx+c的图象经过点A,B.
如图,△OAB中,∠AOB=90°,AO=1,BO=2.以AO为x轴,BO为y轴建立平面直角坐标系,O为原点.二次函数y=x2+bx+c的图象经过点A,B.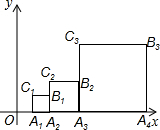 如图,正方形A1A2B1C1,A2A3B2C2,A3A4B3C3,…,AnAn+1BnCn,如图位置依次摆放,已知点C1,C2,C3,…,Cn在直线y=x上,点A1的坐标为(1,0).
如图,正方形A1A2B1C1,A2A3B2C2,A3A4B3C3,…,AnAn+1BnCn,如图位置依次摆放,已知点C1,C2,C3,…,Cn在直线y=x上,点A1的坐标为(1,0). 如图,直角△ABC中,∠ACB=90°,把△ABC绕点C旋转到△DCE,当DC经过AB的中点M时,求证:DE∥BC.
如图,直角△ABC中,∠ACB=90°,把△ABC绕点C旋转到△DCE,当DC经过AB的中点M时,求证:DE∥BC. 如图,在钝角△ABC中,点D是BC的中点,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF,M、N分别为AB、AC的中点,连接DM、DN、DE、DF、EM、EF、FN.求证:
如图,在钝角△ABC中,点D是BC的中点,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF,M、N分别为AB、AC的中点,连接DM、DN、DE、DF、EM、EF、FN.求证: 某天,小华到学校时发现有物品遗忘在家中,此时离上课还有15分钟,于是立即步行回家去取.同时,他爸爸从家里出发骑自行车以他3倍的速度给他送遗忘的物品,两人在途中相遇,相遇后小华立即坐爸爸的自行车赶回学校.爸爸和小华在这个过程中,离学校的路程S(米)与所用时间t(分钟)之间的函数关系如图所示(假设骑自行车和步行的速度始终保持不变).下列说法:
某天,小华到学校时发现有物品遗忘在家中,此时离上课还有15分钟,于是立即步行回家去取.同时,他爸爸从家里出发骑自行车以他3倍的速度给他送遗忘的物品,两人在途中相遇,相遇后小华立即坐爸爸的自行车赶回学校.爸爸和小华在这个过程中,离学校的路程S(米)与所用时间t(分钟)之间的函数关系如图所示(假设骑自行车和步行的速度始终保持不变).下列说法: