题目内容
9.已知矩形ABCD的边AB=2,BC=4,P为矩形ABCD边上的一点,连接AP,若直线AP、BD交点为E,△PAB为等腰三角形,请你画出图形,直接写出AE的长.分析 根据题意画出图形,分两种情况:①当P在BC上时;②当P在CD上时,P为CD的中点;由矩形的性质和勾股定理以及相似三角形的性质即可得出结果.
解答 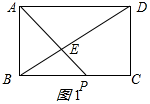 解:分两种情况:
解:分两种情况:
①当P在BC上时,如图1所示
∵四边形ABCD是矩形,
∴∠ABP=90°,AD=BC=4,AD∥BC,CD=AB=2,
∴△ADE∽△PBE,
∴$\frac{AE}{PE}$=$\frac{AD}{PB}$,
∵△ABP是等腰三角形,
∴PB=AB=2,
∴$\frac{AE}{PE}$=2,
∴$\frac{AE}{AP}$=$\frac{2}{3}$,
由勾股定理得:AP=$\sqrt{A{B}^{2}+P{B}^{2}}$=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∴AE=$\frac{4}{3}$$\sqrt{2}$;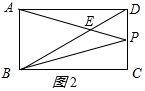
②当P在CD上时,P为CD的中点,如图2所示:
则PD=$\frac{1}{2}$CD=1,
∴AP=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$,
∵AB∥CD,
∴△ABE∽△DPE,
∴$\frac{AE}{PE}=\frac{AB}{PD}$=2,
∴AE=2PE,
∴AE=$\frac{2}{3}$AP=$\frac{2\sqrt{17}}{3}$;
综上所述,AE的长为$\frac{4}{3}$$\sqrt{2}$或$\frac{2\sqrt{17}}{3}$.
点评 本题考查了矩形的性质、等腰三角形的性质、相似三角形的判定与性质、比例的性质;熟练掌握矩形的性质,证明三角形相似得出比例式是解决问题的关键.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
20. 如图,在平行四边形ABCD中,E是CD延长线上一点,BE与AD交于F,若CD=2DE,则$\frac{{S}_{△DEF}}{{S}_{△ABF}}$等于( )
如图,在平行四边形ABCD中,E是CD延长线上一点,BE与AD交于F,若CD=2DE,则$\frac{{S}_{△DEF}}{{S}_{△ABF}}$等于( )
 如图,在平行四边形ABCD中,E是CD延长线上一点,BE与AD交于F,若CD=2DE,则$\frac{{S}_{△DEF}}{{S}_{△ABF}}$等于( )
如图,在平行四边形ABCD中,E是CD延长线上一点,BE与AD交于F,若CD=2DE,则$\frac{{S}_{△DEF}}{{S}_{△ABF}}$等于( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
17.若a满足|2015-a|+$\sqrt{a-2016}$=a,则20152-a的值为( )
| A. | 2015 | B. | -2015 | C. | 2016 | D. | -2016 |
14.在下列表示的不等式的解集中,不包括-5的是( )
| A. | x≤4 | B. | x≥-5 | C. | x≤-6 | D. | x≥-7 |
 如图,两个圆的圆心相同,面积分别为8cm2、18cm2,求圆环的宽度(两圆半径之差,结果保留π).
如图,两个圆的圆心相同,面积分别为8cm2、18cm2,求圆环的宽度(两圆半径之差,结果保留π).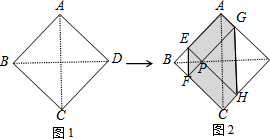 如图1,正方形纸片ABCD边长为2,折叠∠B和∠D,使两个直角的顶点重合于对角线BD上的一点P,EF、GH分别是折痕(图2).设AE=x(0<x<2),给出下列判断:
如图1,正方形纸片ABCD边长为2,折叠∠B和∠D,使两个直角的顶点重合于对角线BD上的一点P,EF、GH分别是折痕(图2).设AE=x(0<x<2),给出下列判断: