题目内容
12.已知$\frac{1}{x}$-$\frac{1}{y}$=$\frac{1}{x-y}$,求$\frac{x}{y}$+$\frac{y}{x}$的值.解:$\frac{1}{x}$-$\frac{1}{y}$=$\frac{1}{x-y}$,
$\frac{y-x}{xy}$=$\frac{1}{x-y}$,即xy=(y-x)2;
∴x2+y2=3xy,从而$\frac{x}{y}$+$\frac{y}{x}$=$\frac{{x}^{2}+{y}^{2}}{xy}$=$\frac{3xy}{xy}$=3.
上述解答过程有无错误?若有误请指出错在哪里?并写出正确答案.
分析 在由$\frac{y-x}{xy}$=$\frac{1}{x-y}$,得出xy=(y-x)2,出现错误,由此进一步改正代入求得答案即可.
解答 解:由$\frac{y-x}{xy}$=$\frac{1}{x-y}$,xy=(y-x)2错误,
∵$\frac{y-x}{xy}$=$\frac{1}{x-y}$,
∴xy=-(y-x)2,
∴x2+y2=xy,
∴$\frac{x}{y}$+$\frac{y}{x}$=$\frac{{x}^{2}+{y}^{2}}{xy}$=1.
点评 此题考查分式的化简求值,掌握计算方法,注意符号的确定是解决问题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
10.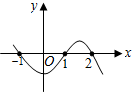 已知y关于x的函数图象如图所示,则当y<0时,自变量x的取值范围是( )
已知y关于x的函数图象如图所示,则当y<0时,自变量x的取值范围是( )
 已知y关于x的函数图象如图所示,则当y<0时,自变量x的取值范围是( )
已知y关于x的函数图象如图所示,则当y<0时,自变量x的取值范围是( )| A. | x<0 | B. | x<-1或1<x<2 | C. | -1<x<1或x>2 | D. | x>-1 |
 如图是一个程序计算器,现输入m=-6,那么输出的结果是25.
如图是一个程序计算器,现输入m=-6,那么输出的结果是25. 如图,五边形ABCDE和五边形JFGHI相似,求角α,β的大小和x,y,z的值.
如图,五边形ABCDE和五边形JFGHI相似,求角α,β的大小和x,y,z的值.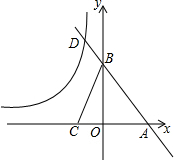 如图,直线AB与x轴、y轴分别交于点A、点B,与双曲线y=$\frac{k}{x}$(x<0)交于点D,点C在x轴上,连接CB,tanC=3,且AB=3DB,线段OA、OC(OA>OC)的长是一元二次方程x2-4x+3=0的两根.
如图,直线AB与x轴、y轴分别交于点A、点B,与双曲线y=$\frac{k}{x}$(x<0)交于点D,点C在x轴上,连接CB,tanC=3,且AB=3DB,线段OA、OC(OA>OC)的长是一元二次方程x2-4x+3=0的两根.