题目内容
如图，线段AD把△ABC分为面积相等的两部分，则线段AD是（ ）．
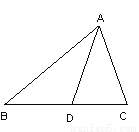
A. 三角形的角平分线 B. 三角形的中线
C. 三角形的高 D. 以上都不对
B
【解析】试题分析：三角形的中线将三角形的面积分成相等的两部分，角平分线是指将角分成度数相等的两个角.
练习册系列答案
相关题目
已知：a、b、c是△ABC三边长，且M=(a＋b＋c)(a＋b－c)(a－b－c)，那么 ( )
A. M＞0 B. M=0 C. M＜0 D. 不能确定
C
【解析】试题解析：∵a、b、c是△ABC三边长，
∴a+b+c>0，a+b?c>0，a?b?c<0，
∴M=(a+b+c)(a+b?c)(a?b?c)<0.
故选C. 一个不透明的盒子中装有10个黑球和若干个白球，它们除颜色不同外，其余均相同，从盒子中随机摸出一球记下其颜色，再把它放回盒子中摇匀，重复上述过程，共试验400次，其中有240次摸到白球，由此估计盒子中的白球大约有________个．
15
【解析】试题解析：∵共试验400次，其中有240次摸到白球，
∴白球所占的比例为，
设盒子中共有白球x个，则，
解得：x=15． 如图，已知在△ABC中，AD⊥BC于点D，AE平分∠BAC，判断∠EAD与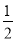
(∠C－∠B)的关系，并说明理由．
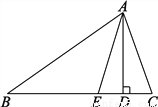
∠EAD= (∠C－∠B)．理由见解析
【解析】试题分析：根据三角形内角和定理求出求出∠DAC和∠EAC，相减即可得出答案．
试题解析：
理由是：
∵AE平分∠BAC，
∵AD⊥BC， 如图所示， AB=AC，AD=AE，∠BAC=∠DAE，∠1=25°，∠2=30°，则∠3=_____.
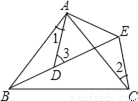
55°
【解析】求出∠BAD=∠EAC，证△BAD≌△EAC，推出∠2=∠ABD=30°，根据三角形的外角性质求出即可．
【解析】
∵∠BAC=∠DAE，
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC，
∴∠1=∠EAC，
在△BAD和△EAC中，
AB=AC，∠BAD=∠EAC，
∴△BAD≌△EAC（SAS），
∴∠2=∠ABD=30°，
∵... 如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F．
求证：（1）FC＝AD；
（2）AB＝BC＋AD．
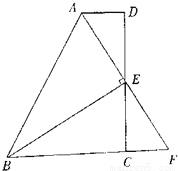
（1）证明见解析；（2）证明见解析.
【解析】试题分析:（1）根据AD∥BC可知∠ADC=∠ECF，再根据E是CD的中点可求出△ADE≌△FCE，根据全等三角形的性质即可解答．
（2）根据线段垂直平分线的性质判断出AB=BF即可．
证明：（1）∵AD∥BC（已知），
∴∠ADC=∠ECF（两直线平行，内错角相等），
∵E是CD的中点（已知），
∴DE=EC（中点... △ABC中，AB = 5，AC = 6，BC = 4，边AB的垂直平分线交AC于点D，则△BDC的周长是（ ）
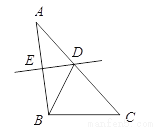
A. 8 B. 9 C. 10 D. 11
C
【解析】试题分析：由ED是AB的垂直平分线，可得AD=BD，又由△BDC的周长=DB+BC+CD，即可得△BDC的周长=AD+BC+CD=AC+BC． ∵ED是AB的垂直平分线， ∴AD=BD，
∵△BDC的周长=DB+BC+CD， ∴△BDC的周长=AD+BC+CD=AC+BC=6+4=10． 如图所示，在Rt△ACD和Rt△BCE中，若AD＝BE，DC＝EC，则无法得出的结论是( )
A. OA＝OB B. E是AC的中点 C. △AOE≌△BOD D. AE＝BD
B
【解析】∵∠C=∠C=90°，
∴△ACD和△BCE是直角三角形，
在Rt△ACD和Rt△BCE中，
∴Rt△ACD≌Rt△BCE（HL），
∴∠B=∠A，CB=CA，
∵CD=CE，
∴AE=BD，故D正确，
在△AOE和△BOD中，
∴△AOE≌△BOD（AAS），故C正确，
∴AO=OB，故A正确，
AE=BD，CE=CD... 如图，若AB∥CD，则∠A、∠E、∠D之间的关系是( )
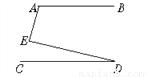
A. ∠A+∠E+∠D=180° B. ∠A－∠E+∠D=180°
C. ∠A+∠E－∠D=180° D. ∠A+∠E+∠D=270°
C
【解析】过点E作EF∥CD，
∵AB∥CD，
∴AB∥EF∥CD，
∴∠AEF=180°-∠A,∠DEF=∠D，
∴∠AED=∠AEF+∠DEF=180°-∠A+∠D；
即∠AED+∠A-∠D =180°.
故选C.