题目内容
16．解不等式组：$\left\{\begin{array}{l}{3（x+2）≥4x+5}\\{\frac{x+1}{2}＞\frac{x}{3}}\end{array}\right.$．分析 首先解每个不等式，两个不等式的解集的公共部分就是不等式组的解集．
解答 解：$\left\{\begin{array}{l}{3（x+2）≥4x+5…①}\\{\frac{x+1}{2}＞\frac{x}{3}…②}\end{array}\right.$，
解①得：x≥-$\frac{1}{2}$，
解②得：x＞-3．
则不等式组的解集是：x≥-$\frac{1}{2}$．
点评 本题考查了一元一次不等式组的解法：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．
练习册系列答案
孟建平名校考卷系列答案
相关题目
7．若关于x的一元二次方程m2x2-（2m-1）x-1=0有两个实数根，则m的取值范围是（ ）
| A． | m$＜\frac{1}{4}$ | B． | m$≤\frac{1}{4}$ | C． | m$≥\frac{1}{4}$ | D． | m$≤\frac{1}{4}$且m≠0 |
4．
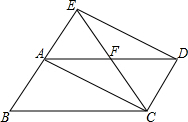如图，将平行四边形ABCD沿对角线AC折叠，点B的对应点落在点E处，且点B、A、E在同一条直线上，CE交AD于点F，连接ED．下列结论中错误的是（ ）
如图，将平行四边形ABCD沿对角线AC折叠，点B的对应点落在点E处，且点B、A、E在同一条直线上，CE交AD于点F，连接ED．下列结论中错误的是（ ）| A． | AF=$\frac{1}{2}BC$ | B． | 四边形ACDE是矩形 | ||
| C． | 图中与△ABC全等的三角形有4个 | D． | 图中有4个等腰三角形 |
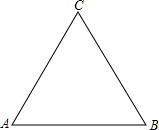已知：如图，等边△ABC中AB=AC=BC=6，请画出△ABC的外接圆⊙O，（要求保留作图痕迹），并计算此外接圆的半径r．
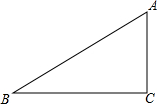已知Rt△ABC中，AC=3，BC=4，翻折使点A和B点重合，尺规作图，画出折痕，折痕交△ABC的两边于点E、F，求EF的长度．
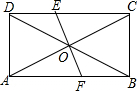如图，在矩形ABCD中，已知AC、BD相交于O，EF⊥AC于O，且交AB于F，交CD于E，EF=AF．