题目内容
5.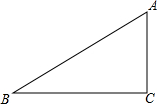 已知Rt△ABC中,AC=3,BC=4,翻折使点A和B点重合,尺规作图,画出折痕,折痕交△ABC的两边于点E、F,求EF的长度.
已知Rt△ABC中,AC=3,BC=4,翻折使点A和B点重合,尺规作图,画出折痕,折痕交△ABC的两边于点E、F,求EF的长度.
分析 作线段AB的垂直平分线交AB于E交BC于F,根据勾股定理得到AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,由折叠的性质得到EF⊥AB,AE=BE=$\frac{1}{2}$AB=$\frac{5}{2}$,根据相似三角形的性质得到$\frac{EF}{AC}=\frac{BE}{BC}$,即可得到结论.
解答 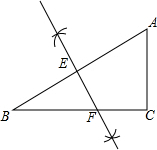 解:如图所示,
解:如图所示,
∵在Rt△ABC中,AC=3,BC=4,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,
∵翻折使点A和B点重合,
∴EF⊥AB,AE=BE=$\frac{1}{2}$AB=$\frac{5}{2}$,
∵∠BEF=∠C=90°,∠B=∠B,
∴△BEF∽△BCA,
∴$\frac{EF}{AC}=\frac{BE}{BC}$,
即$\frac{EF}{3}=\frac{\frac{5}{2}}{4}$,
∴EF=$\frac{15}{8}$.
点评 本题考查了折叠的性质,相似三角形的判定和性质,勾股定理,正确的作出图形是解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
17.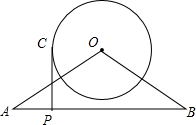 如图,在△OAB中,OA=OB=13,AB=24,以O为圆心,4为半径作⊙O,P为线段AB上动点(从A运动到B),过P作⊙O的切线PC,切点为C,则PC的取值范围是( )
如图,在△OAB中,OA=OB=13,AB=24,以O为圆心,4为半径作⊙O,P为线段AB上动点(从A运动到B),过P作⊙O的切线PC,切点为C,则PC的取值范围是( )
 如图,在△OAB中,OA=OB=13,AB=24,以O为圆心,4为半径作⊙O,P为线段AB上动点(从A运动到B),过P作⊙O的切线PC,切点为C,则PC的取值范围是( )
如图,在△OAB中,OA=OB=13,AB=24,以O为圆心,4为半径作⊙O,P为线段AB上动点(从A运动到B),过P作⊙O的切线PC,切点为C,则PC的取值范围是( )| A. | 3≤PC≤3$\sqrt{17}$ | B. | 5≤PC≤13 | C. | 4≤PC≤3$\sqrt{17}$ | D. | 1<PC≤13 |
 如图,点M、N分别在直线a、b上,且a∥b,P为两平行线间一点,那么∠1+∠2+∠3=360°.
如图,点M、N分别在直线a、b上,且a∥b,P为两平行线间一点,那么∠1+∠2+∠3=360°.
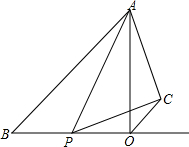 在Rt△AOB中,∠AOB=90°,OA=OB=4厘米,点P从B出发,以1厘米/秒的速度沿射线BO运动,设点P运动时间为t(t>0)秒.△APC是以AP为斜边的等腰直角三角形,且C,O两点在直线AB的同侧,连接OC.
在Rt△AOB中,∠AOB=90°,OA=OB=4厘米,点P从B出发,以1厘米/秒的速度沿射线BO运动,设点P运动时间为t(t>0)秒.△APC是以AP为斜边的等腰直角三角形,且C,O两点在直线AB的同侧,连接OC.