题目内容
11．
已知：如图，等边△ABC中AB=AC=BC=6，请画出△ABC的外接圆⊙O，（要求保留作图痕迹），并计算此外接圆的半径r．
分析 分别作AB和BC的垂直平分线，两垂直平分线相交于点O，然后以O为圆心，OA为半径即可作出△ABC的外接圆⊙O；求出AM=3，由三角函数求出OA即可．
解答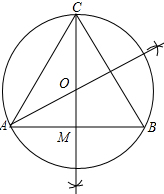 
解：如图所示：
∵△ABC是等边三角形，
∴AM=$\frac{1}{2}$AB=3，∠OAM=$\frac{1}{2}$∠BAC=30°，∠OMA=90°，
∴OA=$\frac{AM}{cos30°}$=$\frac{3}{\frac{\sqrt{3}}{2}}$=2$\sqrt{3}$，
即△ABC的外接圆的半径为$2\sqrt{3}$．
点评 本题考查了作图-复杂作图、等边三角形的性质、三角函数、线段垂直平分线；熟练掌握等边三角形的性质是解决问题的关键．
练习册系列答案
相关题目
1．下列约分正确的是（ ）
| A． | $\frac{{x}^{6}}{{x}^{2}}$=x3 | B． | $\frac{x-y}{x-y}$=0 | C． | $\frac{x-y}{{x}^{2}-xy}$=$\frac{1}{x}$ | D． | $\frac{2{x}^{2}y}{4x{y}^{2}}$=$\frac{1}{2}$ |
如图，在△ABC，AB=AC=2，△ABC=30°，点P、Q分别在边AB、AC上，将△APQ沿PQ翻折，点A落到点A′处，则线段BA′长度的最小值是2$\sqrt{3}$-2．
19．
如图，梯形ABCD中，AD∥BC，AB=DC，∠DBC=45°，点E在BC上，点F在AB上，将梯形ABCD沿直线EF翻折，使得点B与点D重合．如果$\frac{AD}{BC}=\frac{1}{4}$，那么$\frac{AF}{BF}$的值是（ ）
如图，梯形ABCD中，AD∥BC，AB=DC，∠DBC=45°，点E在BC上，点F在AB上，将梯形ABCD沿直线EF翻折，使得点B与点D重合．如果$\frac{AD}{BC}=\frac{1}{4}$，那么$\frac{AF}{BF}$的值是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{3}{5}$ | C． | $\frac{2}{3}$ | D． | $\frac{{\sqrt{2}}}{2}$ |
在数学实践活动课中，小辉利用自己制作的一把“直角角尺”测量、计算一些圆的直径，如图，直角角尺，∠AOB=90°，将点O放在圆周上，分别确定OA、OB与圆的交点C、D，读得数据OC=8，OD=9，则此圆的直径约为（ ）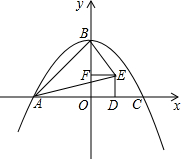
如图，二次函数y=-$\frac{1}{k}$x2+k（k＞0）的图象与x轴相交于A、C两点（点A在点C的左侧），与y轴交于点B，点D为线段OC上一点（不与点O、C重合），以OD为边向上作正方形ODEF，连接AE，BE，AB，AB，设点D的横坐标为m．