题目内容
18.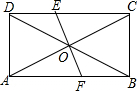 如图,在矩形ABCD中,已知AC、BD相交于O,EF⊥AC于O,且交AB于F,交CD于E,EF=AF.
如图,在矩形ABCD中,已知AC、BD相交于O,EF⊥AC于O,且交AB于F,交CD于E,EF=AF.(1)求∠OFA的度数;
(2)求证:OF=FB.
分析 (1)由矩形的性质得出OA=OB,∠OCE=∠OAF,由ASA证明△OCE≌△OAF,得出OE=OF,证出AF=2OF,由EF⊥AC得出∠OAF=30°,即可得出结果;
(2)由等腰三角形的性质得出∠OBF=∠OAF=30°,由三角形的外角性质得出∠BOF=∠OBF,即可得出结论.
解答 (1)解:∵四边形ABCD是矩形,
∴AB∥CD,OA=OC=$\frac{1}{2}$AC,
,OB=OD=$\frac{1}{2}$BD,AC=BD,
∴OA=OB,
∴∠OCE=∠OAF,
在△OCE和△OAF中,$\left\{\begin{array}{l}{∠OCE=∠OAF}&{\;}\\{OC=OA}&{\;}\\{∠COE=∠AOF}&{\;}\end{array}\right.$,
∴△OCE≌△OAF(ASA),
∴OE=OF,
∵EF=AF,
∴AF=2OF,
∵EF⊥AC,
∴∠AOF=90°,
∴∠OAF=30°,
∴∠OFA=90°-30°=60°;
(2)证明:∵OA=OB,
∴∠OBF=∠OAF=30°,
∵∠OFA=∠OBF+∠BOF,
∴∠BOF=30°=∠OBF,
∴OF=FB.
点评 本题考查了矩形的性质,等腰三角形的性质与判定、全等三角形的判定与性质、三角形的外角性质;熟练掌握矩形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
17.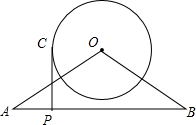 如图,在△OAB中,OA=OB=13,AB=24,以O为圆心,4为半径作⊙O,P为线段AB上动点(从A运动到B),过P作⊙O的切线PC,切点为C,则PC的取值范围是( )
如图,在△OAB中,OA=OB=13,AB=24,以O为圆心,4为半径作⊙O,P为线段AB上动点(从A运动到B),过P作⊙O的切线PC,切点为C,则PC的取值范围是( )
 如图,在△OAB中,OA=OB=13,AB=24,以O为圆心,4为半径作⊙O,P为线段AB上动点(从A运动到B),过P作⊙O的切线PC,切点为C,则PC的取值范围是( )
如图,在△OAB中,OA=OB=13,AB=24,以O为圆心,4为半径作⊙O,P为线段AB上动点(从A运动到B),过P作⊙O的切线PC,切点为C,则PC的取值范围是( )| A. | 3≤PC≤3$\sqrt{17}$ | B. | 5≤PC≤13 | C. | 4≤PC≤3$\sqrt{17}$ | D. | 1<PC≤13 |
3.点O是矩形ABCD内任意一点,点O到点A、B、C的距离分别为a、b、c,那么点O到点D的距离为( )
| A. | $\sqrt{{a}^{2}+{b}^{2}+{c}^{2}}$ | B. | $\sqrt{{a}^{2}-{b}^{2}-{c}^{2}}$ | C. | $\sqrt{{a}^{2}-{b}^{2}+{c}^{2}}$ | D. | $\sqrt{-{c}^{2}+{b}^{2}+{a}^{2}}$ |
10.下列表示y是x的函数的图象是( )
| A. |  | B. |  | C. |  | D. |  |
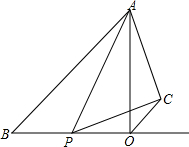 在Rt△AOB中,∠AOB=90°,OA=OB=4厘米,点P从B出发,以1厘米/秒的速度沿射线BO运动,设点P运动时间为t(t>0)秒.△APC是以AP为斜边的等腰直角三角形,且C,O两点在直线AB的同侧,连接OC.
在Rt△AOB中,∠AOB=90°,OA=OB=4厘米,点P从B出发,以1厘米/秒的速度沿射线BO运动,设点P运动时间为t(t>0)秒.△APC是以AP为斜边的等腰直角三角形,且C,O两点在直线AB的同侧,连接OC.