Question

9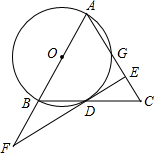．如图，在△ABC中，AB=AC，以AB为直径作⊙O，交BC边于边D，交AC边于点G，过D作⊙O的切线EF，交AB的延长线于点F，交AC于点E．
（1）求证：BD=CD；
（2）若AE=6，BF=4，求⊙O的半径．

Answer 1

分析 （1）连接AD，根据等腰三角形三线合一即可证明．
（2）设⊙O的半径为R，则FO=4+R，FA=4+2R，OD=R，连接OD，由△FOD∽△FAE，得$\frac{OD}{AE}$=$\frac{FO}{AF}$列出方程即可解决问题．

解答 （1）证明：连接AD，
∵AB是直径，
∴∠ADB=90°，
∵AB=AC，AD⊥BC，
∴BD=DC．

（2）解：设⊙O的半径为R，则FO=4+R，FA=4+2R，OD=R，连接OD、
∵AB=AC，
∴∠ABC=∠C，
∵OB=OD，
∴∠ABC=∠ODB，
∴∠ODB=∠C，
∴OD∥AC，
∴△FOD∽△FAE，
∴$\frac{OD}{AE}$=$\frac{FO}{AF}$，
∴$\frac{R}{6}$=$\frac{4+R}{4+2R}$，
整理得R²-R-12=0，
∴R=4或（-3舍弃）．
∴⊙O的半径为4．

点评 本题考查切线的性质、等腰三角形的性质等知识，解题的关键是学会添加常用辅助线，利用相似三角形的性质解决问题，属于中考常考题型．