题目内容
1. 如图,已知Rt△ABC中,∠C=90°,∠A=30°,AB=4.
如图,已知Rt△ABC中,∠C=90°,∠A=30°,AB=4.(1)作AC边上的垂直平分线DE,交AC于点D,交AB于点E(用尺规作图法,保留作图痕迹,不要求写作法和证明):
(2)连接CE,求△BEC的周长.
分析 (1)利用基本作图作AC的垂直平分线得到DE;
(2)先利用含30度的直角三角形三边的关系得到BC=2,再根据线段垂直平分线的性质得到EC=EA,然后利用等线段代换得到△BEC的周长=AB+BC=6.
解答 解:(1)如图,DE为所作;
(2)∵,∠C=90°,∠A=30°,AB=4.
∴BC=$\frac{1}{2}$AB=2,
∵DE垂直平分AC,
∴EC=EA,
∴△BEC的周长=BE+EC+BC
=BE+EA+BC
=AB+BC
=4+2
=6.
点评 本题考查了作图-基本作图:掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).记住含30度的直角三角形三边的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.以下列各组数据作为三角形的三边长,能构成直角三角形的是( )
| A. | 5,6,7 | B. | 7,8,10 | C. | 5,12,13 | D. | 8,16,17. |
10. 如图,平行四边形ABCD的周长为30cm,AB≠AD,AC、BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长为( )
如图,平行四边形ABCD的周长为30cm,AB≠AD,AC、BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长为( )
 如图,平行四边形ABCD的周长为30cm,AB≠AD,AC、BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长为( )
如图,平行四边形ABCD的周长为30cm,AB≠AD,AC、BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长为( )| A. | 10cm | B. | 15cm | C. | 20cm | D. | 30cm |
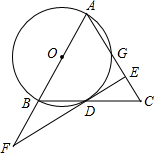 如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC边于边D,交AC边于点G,过D作⊙O的切线EF,交AB的延长线于点F,交AC于点E.
如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC边于边D,交AC边于点G,过D作⊙O的切线EF,交AB的延长线于点F,交AC于点E. 小明所在数学兴趣小组,计划用尺规作图作直角三角形,且这个直角三角形的一条边为2倍的单位长度,另一条边为4倍的单位长度.
小明所在数学兴趣小组,计划用尺规作图作直角三角形,且这个直角三角形的一条边为2倍的单位长度,另一条边为4倍的单位长度. 如图,四边形ABCD是⊙O的内接四边形,若∠C=65°,则∠A=115°.
如图,四边形ABCD是⊙O的内接四边形,若∠C=65°,则∠A=115°. 如图B点在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B北偏东80°方向,则∠ACB=85°.
如图B点在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B北偏东80°方向,则∠ACB=85°.