题目内容

1．如果（x-2）（x+1）=x2+mx+n，那么m+n的值为（　　）
A．-1B．1C．-3D．3

分析 根据多项式乘多项式法则把等式的左边展开，根据题意求出m、n的值，计算即可．

解答 解：（x-2）（x+1）=x2+x-2x-2=x2-x-2，
则m=-1，n=-2，
∴m+n=-3，
故选：C．

点评 本题考查的多项式与多项式相乘的法则：多项式与多项式相乘，先用一个多项式的每一项乘另外一个多项式的每一项，再把所得的积相加．

练习册系列答案
相关题目
11．下列等式中成立的是（　　）
A．a4•a=a4B．a6-a3=a3C．（a3）2=a6D．（ab2）3=a3•b5
12．【定义】如图1，在四边形ABCD中，点E在边BC上（不与点B，C重合），连接AE，DE，
四边形ABCD分成三个三角形：△ABE，△AED和△ECD，如果其中有△ABE与△ECD相似，我们就把点E叫做四边形ABCD在边BC上的相似点；如果这三个三角形都相似，我们就把点E叫做四边形ABCD在边BC上的完美相似点．
【解决问题】如图2，在平面直角坐标系中，过点A（6，0）作x轴的垂线交二次函数y=$\frac{1}{2}$x2-2x-4的图象于点B．
（1）写出点B的坐标；
（2）点P是线段OA上的一个动点（不与点O，A重合），PC⊥PB交y轴于点C．求证：点P是四边形ABCO在边OA 上的相似点；
（3）在四边形ABCO中，当点P是OA边上的完美相似点时，写出点P的坐标．
9．计算：${（-2016）^0}+{（{\frac{1}{4}}）^{-1}}-{（-2）^2}$．
16．化简求值：（x-1）2-（x+2）（x-2）+（x-4）（x+5），其中x2-x-5=0．
4．要组织一次篮球联赛，赛制为单循环形式（每两队之间都赛一场），计划安排21场比赛．若设参赛球队的个数是x个，则可列方程（　　）
A．x（x-1）=21B．x（x+1）=21C．$\frac{x（x-1）}{2}=21$D．$\frac{x（x+1）}{2}=21$
11．边长为2的等边三角形ABC，绕点A旋转120°，则BC边上的中点D转过的路程是$\frac{2\sqrt{3}}{3}$π．
8．已知等腰三角形的两边长分别为4cm、8cm，则该等腰三角形的周长是（　　）
A．12cmB．16cmC．16cm或20cmD．20cm
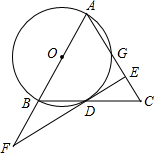9．如图，在△ABC中，AB=AC，以AB为直径作⊙O，交BC边于边D，交AC边于点G，过D作⊙O的切线EF，交AB的延长线于点F，交AC于点E．
（1）求证：BD=CD；
（2）若AE=6，BF=4，求⊙O的半径．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网