Question

7．如图，四边形ABCD为菱形，对角线AC，BD相交于点E，F是边BA延长线上一点，连接EF，以EF为直径作⊙O，交DC于D，G两点，AD分别于EF，GF交于I，H两点．
（1）试判断四边形FACD的形状，并证明你的结论；
（2）当G为线段DC的中点时，设AC=2m，BD=2n，求⊙O的面积与菱形ABCD的面积之比．

Answer 1

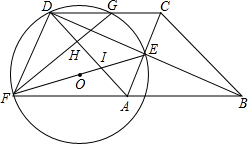
分析 （1）结论：四边形FACD是平行四边形．只要证明AD∥AC，CD∥AF即可．
（2）连接GE，由△EFG∽△CDE，推出$\frac{EF}{CD}$=$\frac{EG}{EC}$，求出EF，即可解决问题．

解答 解：（1）结论：四边形FACD是平行四边形．
理由：∵四边形ABCD是菱形，
∴BD⊥AC，CD∥AB，
∴∠AEB=90°，
∵EF是直径，
∴∠FDE=∠AEB=90°，
∴AD∥AC，∵CD∥AF，
∴四边形FACD是平行四边形．

（2）如图，连接EG．
∵EF是直径，
∴∠EGF=90°，
四边形ABCD是菱形，
∴AC⊥BD，
∴∠EGF=∠DEC=90°，
∵∠EFG=∠EDC，
∴△EFG∽△CDE，
∴$\frac{EF}{CD}$=$\frac{EG}{EC}$，
∵DG=GC，
∴GE=DG=GC=$\frac{1}{2}$CD=$\frac{1}{2}$$\sqrt{{m}^{2}+{n}^{2}}$，
∴$\frac{EF}{\sqrt{{m}^{2}+{n}^{2}}}$=$\frac{\frac{1}{2}\sqrt{{m}^{2}+{n}^{2}}}{m}$，
∴EF=$\frac{{m}^{2}+{n}^{2}}{2m}$，
∴⊙O的面积与菱形ABCD的面积之比=π（$\frac{{m}^{2}+{n}^{2}}{4m}$）²÷2mn=$\frac{π（{m}^{2}+{n}^{2}）}{32{m}^{3}n}$．

点评 本题考查菱形的性质、圆的有关知识、相似三角形的判定和性质、平行四边形顶点等知识，解题的关键是灵活应用这些知识解决问题，属于中考常考题型．