题目内容
8.已知,关于x的不等式组$\left\{\begin{array}{l}{x-a>0}\\{2-x>0}\end{array}\right.$的正整数解共有2个,那么a的取值范围是-1≤a<0.分析 首先解不等式组,利用a表示出不等式组的解集,然后根据不等式组有2个整数解,即可确定整数解,进而求得a的范围.
解答 解:不等式组$\left\{\begin{array}{l}{x-a>0}\\{2-x>0}\end{array}\right.$得解集是a<x<2.
∵不等式组$\left\{\begin{array}{l}{x-a>0}\\{2-x>0}\end{array}\right.$的正整数解共有2个,
∴整数解是1,0.
则-1≤a<0.
故答案是:-1≤a<0.
点评 本题考查了不等式组的整数解,求不等式组的解集应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
18.下列图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16.若点A(a,-3)在y轴上,则点B(a-2,a+3)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.已知:a=$\frac{1}{2-\sqrt{3}}$,b=$\frac{1}{2+\sqrt{3}}$,则a与b的关系是( )
| A. | 相等 | B. | 互为相反数 | C. | 互为倒数 | D. | 平方相等 |
18.计算$\sqrt{10}$×$\sqrt{2}$的结果是( )
| A. | 2$\sqrt{5}$ | B. | 4$\sqrt{5}$ | C. | 5$\sqrt{2}$ | D. | 2$\sqrt{10}$ |
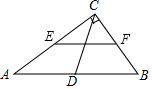 如图,在直角三角形ABC中,∠ACB=90°,D,E,F分别是AB,AC,BC的中点,若CD=5,则EF的长为5.
如图,在直角三角形ABC中,∠ACB=90°,D,E,F分别是AB,AC,BC的中点,若CD=5,则EF的长为5.