题目内容
14.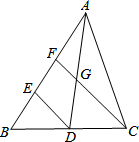 如图,在△ABC中,AD是BC边上的中线,点E、F在AB边上,且E是BF中点,连接DE,CF交AD于G,.
如图,在△ABC中,AD是BC边上的中线,点E、F在AB边上,且E是BF中点,连接DE,CF交AD于G,.(1)求证:△AFG∽△AED;
(2)若FG=3,G为AD中点,求CG的长.
分析 (1)根据AD是BC边上的中线,点E是BF中点,得到BD=CD,BE=EF,根据三角形的中位线的性质得到DE∥CF,即可得到结论;
(2)由G为AD中点,FG∥DE,得到AF=EF,求得DE=2FG=6,根据三角形的中位线的性质得到CF=2DE=12,即可得到结论.
解答 (1)证明:∵AD是BC边上的中线,点E是BF中点,
∴BD=CD,BE=EF,
∴DE是△BCF的中位线,
∴DE∥CF,
∴DE∥FG,
∴△AFG∽△AED;
(2)解:∵G为AD中点,FG∥DE,
∴AF=EF,
∴FG是△ADE的中位线,
∴DE=2FG=6,
∴CF=2DE=12,
∴CG=FC-FG=12-3=9.
点评 本题考查了相似三角形的判定和性质,三角形的中位线的性质,平行线等分线段定理,熟练掌握相似三角形的判定定理是解题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
2.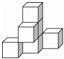 下列图形不是图中几何体的三视图的是( )
下列图形不是图中几何体的三视图的是( )
 下列图形不是图中几何体的三视图的是( )
下列图形不是图中几何体的三视图的是( )| A. | 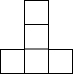 | B. | 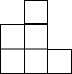 | C. | 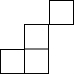 | D. | 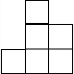 |
 菱形ABCD的边长为6,∠ABC=60°,点P是菱形内一点,且PA=PC=2$\sqrt{3}$
菱形ABCD的边长为6,∠ABC=60°,点P是菱形内一点,且PA=PC=2$\sqrt{3}$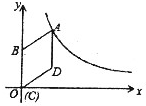 如图,在平面直角坐标系中,菱形ABCD的顶点C与远点O重合,点B在y轴的正半轴上,点A在反比例函数$y=\frac{k}{x}(k>0,x>0)$的图象上,点D的坐标为(4,3),则k的值为( )
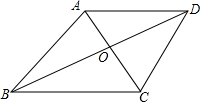
如图,在平面直角坐标系中,菱形ABCD的顶点C与远点O重合,点B在y轴的正半轴上,点A在反比例函数$y=\frac{k}{x}(k>0,x>0)$的图象上,点D的坐标为(4,3),则k的值为( )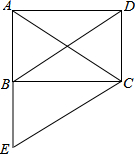 如图,四边形ABCD是矩形,对角线AC、BD相交于点O,CE∥BD,交AB的延长线于点E.
如图,四边形ABCD是矩形,对角线AC、BD相交于点O,CE∥BD,交AB的延长线于点E.