题目内容
9．先化简（$\frac{3}{x-1}$-x-1）÷$\frac{x-2}{{x}^{2}-2x+1}$，再选一个你喜欢的x值代入求值．分析 先根据分式混合运算的法则把原式进行化简，再选取合适的x的值代入进行计算即可．
解答 解：原式=$\frac{4-{x}^{2}}{x-1}$•$\frac{（x-1）^{2}}{x-2}$
=$\frac{-（x+2）（x-2）}{x-1}$•$\frac{{（x-1）}^{2}}{x-2}$
=-（x+2）（x-1），
当x=3时，原式=-5×2=-10．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
备战中考寒假系列答案
相关题目
19．
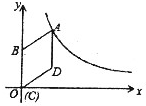如图，在平面直角坐标系中，菱形ABCD的顶点C与远点O重合，点B在y轴的正半轴上，点A在反比例函数$y=\frac{k}{x}（k＞0，x＞0）$的图象上，点D的坐标为（4，3），则k的值为（ ）
如图，在平面直角坐标系中，菱形ABCD的顶点C与远点O重合，点B在y轴的正半轴上，点A在反比例函数$y=\frac{k}{x}（k＞0，x＞0）$的图象上，点D的坐标为（4，3），则k的值为（ ）| A． | 20 | B． | 32 | C． | 24 | D． | 27 |
20．若a=$\sqrt{3b-1}$-$\sqrt{1-3b}$+6，则ab的算术平方根是（ ）
| A． | 2 | B． | $\sqrt{2}$ | C． | ±$\sqrt{2}$ | D． | 4 |
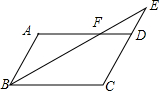如图，平行四边形ABCD中，E是CD的延长线上一点，BE与AD交于点F，若ED：DC=2：3，△DEF的面积为8，则平行四边形ABCD的面积为60．