题目内容
20.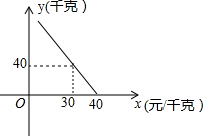 某超市对进货价位20元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
某超市对进货价位20元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
分析 (1)待定系数法求解即可;
(2)设利润为P,根据:总利润=单件利润×销售量列出函数关系式,配方结合函数性质可得函数的最值情况.
解答 解:(1)设y=kx+b,由图象可知,
$\left\{\begin{array}{l}{30k+b=40}\\{40k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-4}\\{b=160}\end{array}\right.$,
则y=-4x+160;
(2)设销售利润为P,根据题意,
得:P=(x-20)(-4x+160)
=-4x2+240x-3200,
=-4(x-30)2+400,
则当x=30时,P最大值=400,
答:当售价为30元/千克时,该品种苹果的每天销售利润最大,最大利润是400元.
点评 本题主要考查二次函数的实际应用能力,待定系数法求解析式是解题的根本,根据函数性质求其最值是关键.

练习册系列答案
 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
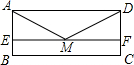 如图,矩形ABCD,E、F在AB、CD上,且EF∥AD,M为EF的中点,连接AM、DM,求证:AM=DM.
如图,矩形ABCD,E、F在AB、CD上,且EF∥AD,M为EF的中点,连接AM、DM,求证:AM=DM. 平面上,将边长相等的正三角形、正方形、正六边形的一边重合并叠在一起,如图,则∠1+∠2+∠3=60°.
平面上,将边长相等的正三角形、正方形、正六边形的一边重合并叠在一起,如图,则∠1+∠2+∠3=60°.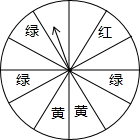 某餐厅为了吸引顾客,举行吃套餐优惠活动,套餐每套20元,每消费一套即可直接获得10元餐劵,或者参与游戏赢得餐劵.游戏规则如下:设立了一个可以自由转动的转盘(如图,转盘被平均分成12份),顾客每消费一套套餐,就可以获得一次转动转盘的机会,如果转盘停止后,指针正好对准红色、黄色、绿色、空白区域,那么顾客就可以分别获得20元、15元、10元、5元餐劵,下次就餐时可以代替现金消费.
某餐厅为了吸引顾客,举行吃套餐优惠活动,套餐每套20元,每消费一套即可直接获得10元餐劵,或者参与游戏赢得餐劵.游戏规则如下:设立了一个可以自由转动的转盘(如图,转盘被平均分成12份),顾客每消费一套套餐,就可以获得一次转动转盘的机会,如果转盘停止后,指针正好对准红色、黄色、绿色、空白区域,那么顾客就可以分别获得20元、15元、10元、5元餐劵,下次就餐时可以代替现金消费.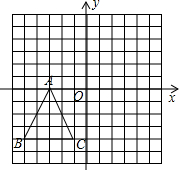 如图,在平面直角坐标系内,△ABC三个顶点的坐标分别为A(-3,0),B(-5,-4),C(-1,-4).
如图,在平面直角坐标系内,△ABC三个顶点的坐标分别为A(-3,0),B(-5,-4),C(-1,-4).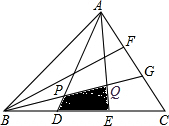 如图,△ABC的面积为1,D,E,F,G分别是BC,AC上的三等分点,求阴影四边形PQED的面积.
如图,△ABC的面积为1,D,E,F,G分别是BC,AC上的三等分点,求阴影四边形PQED的面积.