题目内容
8.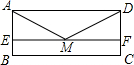 如图,矩形ABCD,E、F在AB、CD上,且EF∥AD,M为EF的中点,连接AM、DM,求证:AM=DM.
如图,矩形ABCD,E、F在AB、CD上,且EF∥AD,M为EF的中点,连接AM、DM,求证:AM=DM.
分析 由矩形的性质得出AE∥DF,∠BAD=90°,再由EF∥AD,证出四边形AEFD是矩形,得出AE=DF,∠AEM=∠DFM=90°,由SAS证明△AEM≌△DFM,得出对应边相等即可.
解答 证明:∵四边形ABCD是矩形,
∴AE∥DF,∠BAD=90°,
∵EF∥AD,
∴四边形AEFD是矩形,
∴AE=DF,∠AEM=∠DFM=90°,
∵M为EF的中点,
∴EM=FM,
在△AEM和△DFM中,$\left\{\begin{array}{l}{AE=DF}&{\;}\\{∠AEM=∠DFM}&{\;}\\{EM=FM}&{\;}\end{array}\right.$,
∴△AEM≌△DFM(SAS),
∴AM=DM.
点评 本题考查了矩形的判定与性质、全等三角形的判定与性质;熟练掌握矩形的判定与性质,证明三角形全等是解决问题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
18.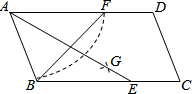 如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为( )
如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为( )
 如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为( )
如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为( )| A. | 16 | B. | 15 | C. | 14 | D. | 13 |
19.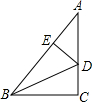 如图,在△ABC中,∠C=90°,AB=5cm,AC=4cm,点D在AC上,将△BCD沿着BD所在直线翻折,使点C落在斜边AB上的点E处,则DC的长为( )
如图,在△ABC中,∠C=90°,AB=5cm,AC=4cm,点D在AC上,将△BCD沿着BD所在直线翻折,使点C落在斜边AB上的点E处,则DC的长为( )
 如图,在△ABC中,∠C=90°,AB=5cm,AC=4cm,点D在AC上,将△BCD沿着BD所在直线翻折,使点C落在斜边AB上的点E处,则DC的长为( )
如图,在△ABC中,∠C=90°,AB=5cm,AC=4cm,点D在AC上,将△BCD沿着BD所在直线翻折,使点C落在斜边AB上的点E处,则DC的长为( )| A. | $\frac{2}{3}$cm | B. | $\frac{3}{2}$cm | C. | 2cm | D. | $\frac{3}{2}\sqrt{5}$cm |
16. 如图是一个三棱柱,它的左视图是( )
如图是一个三棱柱,它的左视图是( )
 如图是一个三棱柱,它的左视图是( )
如图是一个三棱柱,它的左视图是( )| A. |  | B. |  | C. |  | D. |  |
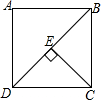 如图,设矩形ABCD的边BC=x,DC=y,连接BD且CE⊥BD,CE=2,BD=4,则(x+y)2-3xy+2的值为10.
如图,设矩形ABCD的边BC=x,DC=y,连接BD且CE⊥BD,CE=2,BD=4,则(x+y)2-3xy+2的值为10.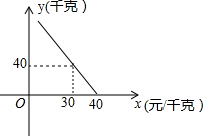 某超市对进货价位20元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
某超市对进货价位20元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.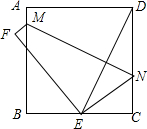 将一张边长为4cm的正方形纸片沿MN对折,使点D落在BC边上.
将一张边长为4cm的正方形纸片沿MN对折,使点D落在BC边上.