题目内容
 如图,在?ABCD中,点E、F、G、H分别是AB、BC、CD、DA的中点,点P在线段GF上,则△PHE与?ABCD的面积的比值是
如图,在?ABCD中,点E、F、G、H分别是AB、BC、CD、DA的中点,点P在线段GF上,则△PHE与?ABCD的面积的比值是考点:平行四边形的性质,三角形的面积,三角形中位线定理,相似三角形的判定与性质
专题:计算题
分析:连接BD,根据三角形中位线得出GF∥BD,HF∥BD,GF=
BD,EH=
BD,推出△CGF∽△CDB,设△CBD的边BD上的高是h,得出平行线BD和GF间的距离是
h,平行线EH和BD间的距离是
h,求出△PHE的边HE上的高,求出平行四边形ABCD的面积和△PHE的面积即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:连接BD,
∵点E、F、G、H分别是AB、BC、CD、DA的中点,
∴GF∥BD,HF∥BD,GF=
BD,EH=
BD,
∴△CGF∽△CDB,
设△CBD的边BD上的高是h,
则平行线BD和GF间的距离是
h,
同理平行线EH和BD间的距离是
h,
∴△PHE的边HE上的高是
h+
h=h,
∴平行四边形ABCD的面积是S△ABD+S△CBD=2S△CBD=2×BD×h×
=BDh,
△PHE的面积是
EH×h=
×
BD×h=
BDh,
∴△PHE与?ABCD的面积的比值
,
故答案为:
.

∵点E、F、G、H分别是AB、BC、CD、DA的中点,
∴GF∥BD,HF∥BD,GF=
| 1 |
| 2 |
| 1 |
| 2 |
∴△CGF∽△CDB,
设△CBD的边BD上的高是h,
则平行线BD和GF间的距离是
| 1 |
| 2 |
同理平行线EH和BD间的距离是
| 1 |
| 2 |
∴△PHE的边HE上的高是
| 1 |
| 2 |
| 1 |
| 2 |
∴平行四边形ABCD的面积是S△ABD+S△CBD=2S△CBD=2×BD×h×
| 1 |
| 2 |
△PHE的面积是
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴△PHE与?ABCD的面积的比值
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:本题考查了平行四边形的性质,三角形的面积,三角形的中位线,相似三角形的性质和判定等知识点的应用,主要培养学生运用定理进行推理的能力,本题题型较好,但有一定的难度.

练习册系列答案
相关题目
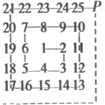 友谊公园有一片长方形竹林,栽了25棵竹子,为了方便管理,每个竹子都有自己的编号,如图所示.标有2、3、5、7、10、13、17、21的竹子都在拐角处,如果P处也栽一棵竹子,编号为26,在此转弯(如虚线),按以上规律继续栽竹子,则第200个拐角处(编号2在第1个拐角处)的竹子的编号应为( )
友谊公园有一片长方形竹林,栽了25棵竹子,为了方便管理,每个竹子都有自己的编号,如图所示.标有2、3、5、7、10、13、17、21的竹子都在拐角处,如果P处也栽一棵竹子,编号为26,在此转弯(如虚线),按以上规律继续栽竹子,则第200个拐角处(编号2在第1个拐角处)的竹子的编号应为( )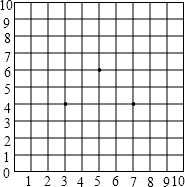 在图的方格棋盘中放入3枚棋子,位置分别是(3,4),(7,4),(5,6).这三枚棋子组成一个什么样的图形?你能不能再放入一枚棋子,使得这四枚棋子组成一个正方形?如果能,请说出放在什么位置.
在图的方格棋盘中放入3枚棋子,位置分别是(3,4),(7,4),(5,6).这三枚棋子组成一个什么样的图形?你能不能再放入一枚棋子,使得这四枚棋子组成一个正方形?如果能,请说出放在什么位置. 如图,⊙O1在⊙O2上无滑动地滚动4周后,刚好回到原来的位置,则⊙O1与⊙O2的面积之比为
如图,⊙O1在⊙O2上无滑动地滚动4周后,刚好回到原来的位置,则⊙O1与⊙O2的面积之比为