题目内容
9.已知x(x-1)-(x2-y)=-2,则$\frac{{x}^{2}+{y}^{2}}{2}$-xy=2.分析 已知的式子可以化成x-y=2的形式,所求的式子可以化成$\frac{1}{2}$(x-y)2代入求解即可.
解答 解:x(x-1)-(x2-y)=-2,
即x2-x-x2+y=-2,
则x-y=2.
故原式=$\frac{1}{2}$(x-y)2=$\frac{1}{2}$×4=2.
故答案是:2.
点评 本题考查了代数式的化简求值,正确利用完全平方公式的变形,把所求的式子化成$\frac{1}{2}$(x-y)2的形式是关键.

练习册系列答案
相关题目
17.如图四个图案中轴对称图形的个数是( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
14.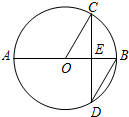 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为3cm,则CD弦长为( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为3cm,则CD弦长为( )
 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为3cm,则CD弦长为( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为3cm,则CD弦长为( )| A. | $\frac{3}{2}$cm | B. | $\frac{3}{2}$$\sqrt{3}$cm | C. | 3$\sqrt{3}$cm | D. | 6cm |
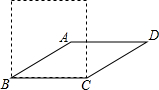 如图,若将四根木条钉成的矩形木框变成平行四边形ABCD的形状,使∠ABC=30°.设矩形面积为s1、平行四边形ABCD面积为s2,则s1与s2的关系为S1=2S2.
如图,若将四根木条钉成的矩形木框变成平行四边形ABCD的形状,使∠ABC=30°.设矩形面积为s1、平行四边形ABCD面积为s2,则s1与s2的关系为S1=2S2.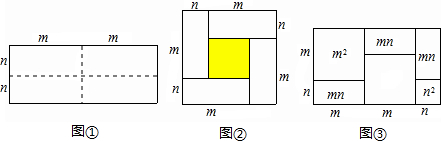
 如图,在平面直角坐标系中,二次函数y=-x2+bx的图象经过点A(4,0).点E是过点C(2,0)且与y轴平行的直线上的一个动点,过线段CE的中点G作DF⊥CE交二次函数的图象于D、F两点.
如图,在平面直角坐标系中,二次函数y=-x2+bx的图象经过点A(4,0).点E是过点C(2,0)且与y轴平行的直线上的一个动点,过线段CE的中点G作DF⊥CE交二次函数的图象于D、F两点.