题目内容
2.先化简,再求值:($\frac{1}{{x}^{2}-2x}$-$\frac{1}{{x}^{2}-4x+4}$)÷$\frac{2}{{x}^{2}-2x}$,其中x=2sin45°+2tan45°.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,利用特殊角的三角函数值求出x的值,代入计算即可求出值.
解答 解:原式=[$\frac{1}{x(x-2)}$-$\frac{1}{(x-2)^{2}}$]•$\frac{x(x-2)}{2}$=$\frac{x-2-x}{x(x-2)^{2}}$•$\frac{x(x-2)}{2}$=-$\frac{1}{x-2}$,
当x=2sin45°+2tan45°=2×$\frac{\sqrt{2}}{2}$+2×1=$\sqrt{2}$+2时,原式=-$\frac{\sqrt{2}}{2}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
12.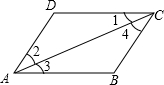 如图所示,下列推理及所注理由正确的是( )
如图所示,下列推理及所注理由正确的是( )
 如图所示,下列推理及所注理由正确的是( )
如图所示,下列推理及所注理由正确的是( )| A. | 因为∠1=∠3,所以AB∥CD(两直线平行,内错角相等) | |
| B. | 因为AB∥CD,所以∠2=∠4(两直线平行,内错角相等) | |
| C. | 因为AD∥BC,所以∠3=∠4(两直线平行,内错角相等) | |
| D. | 因为∠2=∠4,所以AD∥BC(内错角相等,两直线平行) |
10.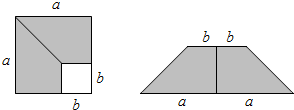 如图,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( )
如图,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( )
 如图,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( )
如图,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( )| A. | (a-b)2=a2-2ab+b2 | B. | (a+b)2=a2+2ab+b2 | C. | a2-b2=(a+b)(a-b) | D. | 无法确定 |
17.如图四个图案中轴对称图形的个数是( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
14.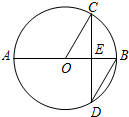 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为3cm,则CD弦长为( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为3cm,则CD弦长为( )
 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为3cm,则CD弦长为( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为3cm,则CD弦长为( )| A. | $\frac{3}{2}$cm | B. | $\frac{3}{2}$$\sqrt{3}$cm | C. | 3$\sqrt{3}$cm | D. | 6cm |
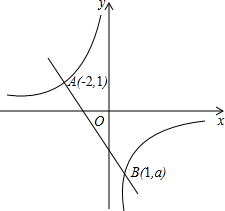 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A(-2,1)、B(1,n)两点.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A(-2,1)、B(1,n)两点. 如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如;当x=1时,y1=0,y2=4,y1<y2,此时M=0,下列判断中正确的是( )
如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如;当x=1时,y1=0,y2=4,y1<y2,此时M=0,下列判断中正确的是( )