题目内容
4.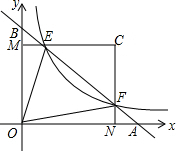 如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,与反比例函数 y=$\frac{k}{x}$(k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若 $\frac{BE}{BF}$=$\frac{1}{4}$,记△CEF的面积为s1,△OEF的面积为s2,则 $\frac{s_1}{s_2}$=( )
如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,与反比例函数 y=$\frac{k}{x}$(k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若 $\frac{BE}{BF}$=$\frac{1}{4}$,记△CEF的面积为s1,△OEF的面积为s2,则 $\frac{s_1}{s_2}$=( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{8}$ |
分析 根据E,F都在反比例函数的图象上得出假设出E,F的坐标,进而分别得出△CEF的面积S1以及△OEF的面积S2,然后即可得出答案.
解答 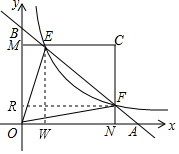 解:过点F作FR⊥MO于点R,EW⊥NO于点W,
解:过点F作FR⊥MO于点R,EW⊥NO于点W,
∵$\frac{BE}{BF}$=$\frac{1}{4}$,
∴$\frac{ME}{FR}$=$\frac{1}{4}$,
∵ME•EW=FR•NF,
∴$\frac{ME}{FR}$=$\frac{FN}{EW}$=$\frac{1}{4}$,
∴S1=$\frac{1}{2}$(4x-x)(4y-y)=$\frac{9}{2}$xy,
设E点坐标为:(x,4y),则F点坐标为:(4x,y),
∵△OEF的面积为:S2=S矩形CNOM-S1-S△MEO-S△FON
=CN•ON-$\frac{9}{2}$xy-$\frac{1}{2}$ME•MO-$\frac{1}{2}$FN•NO
=4x•4y-$\frac{9}{2}$xy-$\frac{1}{2}$x•4y-$\frac{1}{2}$y•4x
=16xy-$\frac{9}{2}$xy-4xy
=$\frac{15}{2}$xy,
∴$\frac{{S}_{1}}{{S}_{2}}$=$\frac{\frac{9}{2}xy}{\frac{15}{2}xy}$=$\frac{3}{5}$.
故选:B.
点评 此题主要考查了反比例函数的综合应用以及三角形面积求法,根据已知表示出E,F的点坐标是解题关键,难度较大,要求同学们能将所学的知识融会贯通.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
16.下列二次根式,不能与$\sqrt{2}$合并的是( )
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\sqrt{8}$ | C. | $\sqrt{12}$ | D. | -$\sqrt{18}$ |
19.下列各式中正确的是( )
| A. | $\sqrt{\frac{a}{2{b}^{2}}}$=$\frac{1}{2b}$$\sqrt{a}$(b>0) | B. | $\sqrt{\frac{7x}{12{y}^{3}}}$=$\frac{1}{6{y}^{2}}$$\sqrt{21xy}$ | ||
| C. | $\sqrt{{a}^{2}+{b}^{2}}$=a+b(a≥0,b≥0) | D. | 5$\sqrt{\frac{2a}{5}}$=$\sqrt{2a}$ |
9.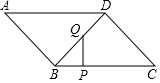 如图,在?ABCD中,BC=20$\sqrt{2}$cm,CD=20cm,∠A=45°,动点P从点B出发,沿BC向点C运动,动点Q从点D出发,沿DB向点B运动,点P和点Q的运动速度分别为3$\sqrt{2}$cm/s和2cm/s,一点停止运动,则另一点也随之停止,当△BPQ是直角三角形时,需要经过( )
如图,在?ABCD中,BC=20$\sqrt{2}$cm,CD=20cm,∠A=45°,动点P从点B出发,沿BC向点C运动,动点Q从点D出发,沿DB向点B运动,点P和点Q的运动速度分别为3$\sqrt{2}$cm/s和2cm/s,一点停止运动,则另一点也随之停止,当△BPQ是直角三角形时,需要经过( )
 如图,在?ABCD中,BC=20$\sqrt{2}$cm,CD=20cm,∠A=45°,动点P从点B出发,沿BC向点C运动,动点Q从点D出发,沿DB向点B运动,点P和点Q的运动速度分别为3$\sqrt{2}$cm/s和2cm/s,一点停止运动,则另一点也随之停止,当△BPQ是直角三角形时,需要经过( )
如图,在?ABCD中,BC=20$\sqrt{2}$cm,CD=20cm,∠A=45°,动点P从点B出发,沿BC向点C运动,动点Q从点D出发,沿DB向点B运动,点P和点Q的运动速度分别为3$\sqrt{2}$cm/s和2cm/s,一点停止运动,则另一点也随之停止,当△BPQ是直角三角形时,需要经过( )| A. | 4s | B. | $\frac{5}{2}$s | C. | $\frac{5}{2}$s或4s | D. | 6s |
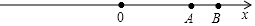 如图,数轴上A,B两点对应的有理数分别为10和15,点P从点B出发,以每秒1个单位长度的速度沿数轴负方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.
如图,数轴上A,B两点对应的有理数分别为10和15,点P从点B出发,以每秒1个单位长度的速度沿数轴负方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.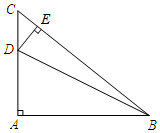 如图,在等腰Rt△ABC中,∠A=90°,AC=6,D是AC上一点,过D作DE⊥BC于点E,若$tan∠DBA=\frac{1}{5}$,则CE的长为$\frac{12\sqrt{2}}{5}$.
如图,在等腰Rt△ABC中,∠A=90°,AC=6,D是AC上一点,过D作DE⊥BC于点E,若$tan∠DBA=\frac{1}{5}$,则CE的长为$\frac{12\sqrt{2}}{5}$.