题目内容
19.下列各式中正确的是( )| A. | $\sqrt{\frac{a}{2{b}^{2}}}$=$\frac{1}{2b}$$\sqrt{a}$(b>0) | B. | $\sqrt{\frac{7x}{12{y}^{3}}}$=$\frac{1}{6{y}^{2}}$$\sqrt{21xy}$ | ||
| C. | $\sqrt{{a}^{2}+{b}^{2}}$=a+b(a≥0,b≥0) | D. | 5$\sqrt{\frac{2a}{5}}$=$\sqrt{2a}$ |
分析 依据二次根式的性质进行化简即可.
解答 解:A、$\sqrt{\frac{a}{2{b}^{2}}}$=$\sqrt{\frac{2a}{4{b}^{2}}}$=$\frac{1}{2b}$$\sqrt{2a}$,故A错误;
B、$\sqrt{\frac{7x}{12{y}^{3}}}$=$\frac{1}{6{y}^{2}}$$\sqrt{21xy}$,故B正确;
C、$\sqrt{{a}^{2}+{b}^{2}}$是一个最简二次根式,故C错误;
D、5$\sqrt{\frac{2a}{5}}$=5$\sqrt{\frac{10a}{25}}$=$\sqrt{10a}$,故D错误.
故选:B.
点评 本题主要考查的是二次根式的性质与化简,熟练掌握二次根式的性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.甲、乙两名运动员在某项射击比赛中10次射击的平均成绩都是7环,而甲、乙的成绩的方差分别为1.21和3.12,由此可知( )
| A. | 甲比乙的成绩稳定 | B. | 乙比甲的成绩稳定 | ||
| C. | 甲、乙的成绩一样稳定 | D. | 无法确定谁的成绩更稳定 |
14.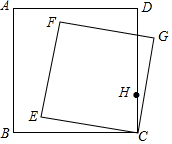 如图,正方形ABCD中,AB=4,点H在CD边上,且CH=1,点E绕点B旋转,同时,以CE为边在BC上方作正方形CEFG,在点E运动过程中,当线段FH取得最小值时,∠CBE的正切为( )
如图,正方形ABCD中,AB=4,点H在CD边上,且CH=1,点E绕点B旋转,同时,以CE为边在BC上方作正方形CEFG,在点E运动过程中,当线段FH取得最小值时,∠CBE的正切为( )
 如图,正方形ABCD中,AB=4,点H在CD边上,且CH=1,点E绕点B旋转,同时,以CE为边在BC上方作正方形CEFG,在点E运动过程中,当线段FH取得最小值时,∠CBE的正切为( )
如图,正方形ABCD中,AB=4,点H在CD边上,且CH=1,点E绕点B旋转,同时,以CE为边在BC上方作正方形CEFG,在点E运动过程中,当线段FH取得最小值时,∠CBE的正切为( )| A. | $\frac{1}{5}$ | B. | $\frac{\sqrt{2}}{5}$ | C. | $\frac{\sqrt{2}}{7}$ | D. | $\frac{1}{7}$ |
4.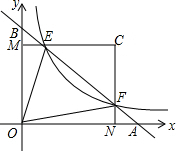 如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,与反比例函数 y=$\frac{k}{x}$(k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若 $\frac{BE}{BF}$=$\frac{1}{4}$,记△CEF的面积为s1,△OEF的面积为s2,则 $\frac{s_1}{s_2}$=( )
如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,与反比例函数 y=$\frac{k}{x}$(k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若 $\frac{BE}{BF}$=$\frac{1}{4}$,记△CEF的面积为s1,△OEF的面积为s2,则 $\frac{s_1}{s_2}$=( )
 如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,与反比例函数 y=$\frac{k}{x}$(k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若 $\frac{BE}{BF}$=$\frac{1}{4}$,记△CEF的面积为s1,△OEF的面积为s2,则 $\frac{s_1}{s_2}$=( )
如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,与反比例函数 y=$\frac{k}{x}$(k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若 $\frac{BE}{BF}$=$\frac{1}{4}$,记△CEF的面积为s1,△OEF的面积为s2,则 $\frac{s_1}{s_2}$=( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{8}$ |
8.某班抽取6名同学参加体能测试,成绩如下:85,90,75,75,80,80.下列表述正确的是( )
| A. | 众数是80 | B. | 中位数是75 | C. | 平均数是80 | D. | 极差是15 |

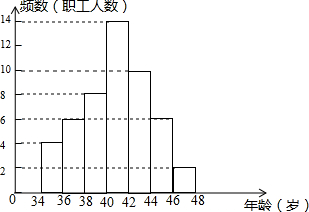 如图是某单位职工年龄(取正整数)的频数分布直方图(每组数据含最小值,不含最大值),则职工人数最多年龄段的职工人数占总人数的百分比为28%.
如图是某单位职工年龄(取正整数)的频数分布直方图(每组数据含最小值,不含最大值),则职工人数最多年龄段的职工人数占总人数的百分比为28%.