题目内容
15.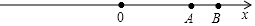 如图,数轴上A,B两点对应的有理数分别为10和15,点P从点B出发,以每秒1个单位长度的速度沿数轴负方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.
如图,数轴上A,B两点对应的有理数分别为10和15,点P从点B出发,以每秒1个单位长度的速度沿数轴负方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.(1)当0<t<5时,用含t的式子填空:
AP=5-t;
AQ=10-2t;
PQ=15-3t.
(2)当t>5时,用含t的式子填空:
AP=t-5;
AQ=2t-10;
PQ=3t-15.
分析 (1)根据题意可知BP=t,OQ=2t,OA=10,AB=5,当0<t<5时,点P在AB之间,点Q在OA之间,再根据线段的和差关系,即可得到线段的表达式;
(2)当t>5时,点P在射线AO上,点Q在射线AB上,再根据线段的和差关系,即可得到线段的表达式.
解答 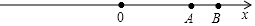 解:(1)由题可得,BP=t,OQ=2t,OA=10,AB=5,
解:(1)由题可得,BP=t,OQ=2t,OA=10,AB=5,
∵当0<t<5时,点P在AB之间,点Q在OA之间,
∴AP=AB-BP=5-t;AQ=OA-OQ=10-2t;
PQ=AP+AQ=15-3t.
故答案为:5-t,10-2t,15-3t;
(2)∵当t>5时,点P在射线AO上,点Q在射线AB上,
∴AP=BP-BA=t-5;
AQ=OQ-OA=2t-10;
PQ=AP+AQ=3t-15.
故答案为:t-5,2t-10,3t-15.
点评 本题主要考查了数轴以及列代数式,解决问题的关键是根据t的大小得到点P和点Q的位置,依据线段的和差关系进行求解.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
4.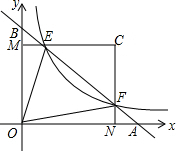 如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,与反比例函数 y=$\frac{k}{x}$(k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若 $\frac{BE}{BF}$=$\frac{1}{4}$,记△CEF的面积为s1,△OEF的面积为s2,则 $\frac{s_1}{s_2}$=( )
如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,与反比例函数 y=$\frac{k}{x}$(k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若 $\frac{BE}{BF}$=$\frac{1}{4}$,记△CEF的面积为s1,△OEF的面积为s2,则 $\frac{s_1}{s_2}$=( )
 如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,与反比例函数 y=$\frac{k}{x}$(k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若 $\frac{BE}{BF}$=$\frac{1}{4}$,记△CEF的面积为s1,△OEF的面积为s2,则 $\frac{s_1}{s_2}$=( )
如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,与反比例函数 y=$\frac{k}{x}$(k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若 $\frac{BE}{BF}$=$\frac{1}{4}$,记△CEF的面积为s1,△OEF的面积为s2,则 $\frac{s_1}{s_2}$=( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{8}$ |
5.在不借助任何工具的情况下,人的眼睛可以看到的最小的物体的大小约为0.00003米,将0.00003用科学记数法表示为( )
| A. | 3×10-5 | B. | 0.3×10-4 | C. | 30×10-6 | D. | 3×105 |
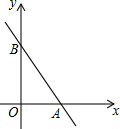 如图,直线y=kx+b与坐标轴交于A(3,0),B(0,5)两点,则不等式kx+b≤0的解集为x≥3.
如图,直线y=kx+b与坐标轴交于A(3,0),B(0,5)两点,则不等式kx+b≤0的解集为x≥3.