如图1是一个长为2m.宽为2n的长方形.沿图中的虚线剪开均分成四个小长方形.然后按图2形状拼成一个正方形．(1)图2中的阴影部分的正方形的边长可表示为(m-n)2或(m+n)2-4mn,(2)观察并分析图2中阴影部分面积的不同表示方法.你能写出(m+n)2.(m-n)2.mn三个代数式之间的等量关系吗?题中等量关系.解决下列问题:若m+n=5.mn=4 题目和参考答案——青夏教育精英家教网——

题目内容

13．如图1是一个长为2m，宽为2n的长方形，沿图中的虚线剪开均分成四个小长方形，然后按图2形状拼成一个正方形．
（1）图2中的阴影部分的正方形的边长可表示为（m-n）²或（m+n）²-4mn；
（2）观察并分析图2中阴影部分面积的不同表示方法，你能写出（m+n）²，（m-n）²，mn三个代数式之间的等量关系吗？
（3）根据（2）题中等量关系，解决下列问题：若m+n=5，mn=4，求m-n的值．

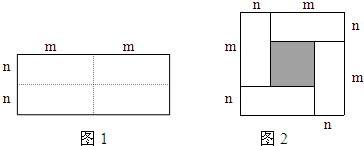
分析（1）根据图形中各个部分的面积得出即可；
（2）根据（1）中的结果即可得出答案；
（3）先根据（2）的结果进行变形，再代入求出即可．

解答解：（1）图中阴影部分的面积为（m-n）²或（m+n）²-4mn，
故答案为：（m-n）²或（m+n）²-4mn；

（2）关系为：（m-n）²=（m+n）²-4mn；

（3）∵m+n=5，mn=4，
∴（m-n）²=（m+n）²-4mn=5²-4×4=9，
∴m-n=±3．

点评本题考查了完全平方公式的应用，能熟记完全平方公式是解此题的关键，注意：（a+b）²=a²+2ab+b²，（a-b）²=a²-2ab+b²，（a-b）²=（a+b）²-4ab．

练习册系列答案

课前课后同步练习系列答案

经纶学典课时作业系列答案

课堂小作业系列答案

黄冈小状元口算速算练习册系列答案

成功训练计划系列答案

倍速训练法直通中考考点系列答案

浙江名卷系列答案

励耘活页系列答案

一卷搞定系列答案

名校作业本系列答案

相关题目

小明和小颖家住在同一地铁站口的同一小区内．星期天两人各自去南禅寺书城买书．小颖乘地铁，小明由爸爸开私家车前往．已知该段私家车行驶的路线和地铁路线恰好在同一直线上，且私家车的速度比地铁慢．他们早上同时出发，设出发后的时间为t分钟，小明和小颖之间的距离为S，S与t的部分函数图象如图所示．
（1）填空：
该小区与南禅寺相距22千米．
私家车的速度为1千米/分钟，地铁的速度为2千米/分钟，
图中点A的实际意思是：小颖乘地铁用11分钟到达南禅寺，此时与小明相距11千米
（2）如果小明到达书城后半小时，两人同时回家，小颖马上乘上了地铁，而小明的爸爸去停车场取车耗费了5分钟，请在原坐标系中将S与t的函数图象补充完整（需要标明相关数据）

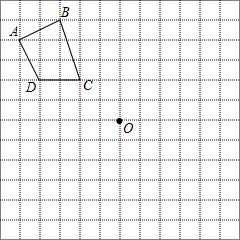如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点四边形ABCD（顶点是网格线的交点）和格点O．
（1）把四边形ABCD平移，使得顶点C与O重合，画出平移后得到的四边形A₂B₁C₁D₁；
（2）把四边形ABCD绕O点顺时针旋转90°，画出旋转后得到的四边形A₂B₂C₂D₂．

1．若x₁、x₂是关于x的一元二次方程ax²+bx+c=0（a≠0）的两个根，则方程的两个根x₁、x₂和系数a、b、c有如下关系：x₁+x₂=-$\frac{b}{a}$，x₁•x₂=$\frac{c}{a}$，我们把它们称为根与系数的关系定理，请你参考上述定理，解答下列问题：
设二次函数y=ax²+bx+c（a≠0）的图象与x轴的两个交点为A（x₁，0），B（x₂，0）．抛物线的顶点为C，且△ABC为等腰三角形．
（1）求A、B两点之间的距离（用字母a、b、c表示）
（2）当△ABC为等腰直角三角形时，求b²-4ac的值；
（3）设抛物线y=x²+kx+1与x轴的两个交点为A、B，顶点为C，且∠ACB=90°，试问如何平移此抛物线，才能使∠ACB=60°？

8．根据要求，回答以下问题：
（1）如图1，正方形ABCD中，对角线AC、BD交于点O，点E是BO上的一点，BG垂直AE于F，交AC于点G．请你直接写出AE、BG以及OE、OG的大小关系是：AE=BG，OE=OG．
（2）如图2，菱形ABCD中，对角线AC、BD交于点O，点E是BO上的一点，BG垂直AE于F，交AC于点G，且AC=6，BD=8，请你求出AE、BG的数量关系．
（3）如图3，?ABCD中，对角线AC、BD交于点O，AC=8，BD=24，∠AOB=60°，点E是BO上的一点，OE=1，点G在对角线AC所在的直线上，当OG=3或9时，AE：BG=1：3．

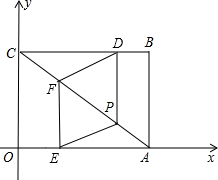在直角坐标系中，点O为原点，点B的坐标为（4，3），四边形ABCO是矩形，点D从B出发以每秒1个单位的速度向终点C运动，同时点E从O点出发以每秒1个单位的速度向终点A运动，过D作DP⊥BC与AC交于点P，过E作EF⊥AO与AC交于点F，连结DF、PE．
（1）求出直线AC的解析式，若动点D运动t秒，写出P点的坐标（用含t的代数式表示）；
（2）当t＜2时，四边形EFDP能否是菱形？若能，则求t的值；若不能，请说明理由；
（3）设四边形COEP的面积为S，请写出S与t的函数关系式，并求出S的最小值；
（4）△APE能否是等腰三角形？若能，请直接写出此时P点的坐标．

如图，已知抛物线y=ax²-x+c经过点Q （-2，4），且它的顶点P的横坐标为-1．设抛物线与x轴相交于A，B两点，
（1）求抛物线的解析式；
（2）求A，B两点的坐标；
（3）设PB与y轴交于C点，求△ABC的面积．

如图，一次函数y=$\frac{1}{2}$x+2的图象与x轴交于点B，与反比例函数y=$\frac{k}{x}$（k≠0）的图象的一个交点为A（2，m）．
（1）求反比例函数的表达式；
（2）过点A作AC⊥x轴，垂足为点C，设点D在反比例函数图象上，且△DBC的面积等于6，请求出点D的坐标；
（3）请直接写出不等式$\frac{1}{2}$x+2＜$\frac{k}{x}$成立的x取值范围．

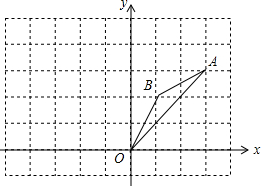如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，3），B（1，2），△AOB绕点O逆时针旋转90°后得到△A₁OB₁．
（1）画出△A₁OB₁，直接写出点B₁关于点O的对称点B₂的坐标；
（2）请直接写出：以A、B、O、C为顶点的平行四边形的第四个顶点C的坐标；
（3）请直接写出：在旋转过程中，点B经过的路径的长；
（4）求在旋转过程中，线段AB所扫过的面积．