题目内容
3. 小明和小颖家住在同一地铁站口的同一小区内.星期天两人各自去南禅寺书城买书.小颖乘地铁,小明由爸爸开私家车前往.已知该段私家车行驶的路线和地铁路线恰好在同一直线上,且私家车的速度比地铁慢.他们早上同时出发,设出发后的时间为t分钟,小明和小颖之间的距离为S,S与t的部分函数图象如图所示.
小明和小颖家住在同一地铁站口的同一小区内.星期天两人各自去南禅寺书城买书.小颖乘地铁,小明由爸爸开私家车前往.已知该段私家车行驶的路线和地铁路线恰好在同一直线上,且私家车的速度比地铁慢.他们早上同时出发,设出发后的时间为t分钟,小明和小颖之间的距离为S,S与t的部分函数图象如图所示.(1)填空:
该小区与南禅寺相距22千米.
私家车的速度为1千米/分钟,地铁的速度为2千米/分钟,
图中点A的实际意思是:小颖乘地铁用11分钟到达南禅寺,此时与小明相距11千米
(2)如果小明到达书城后半小时,两人同时回家,小颖马上乘上了地铁,而小明的爸爸去停车场取车耗费了5分钟,请在原坐标系中将S与t的函数图象补充完整(需要标明相关数据)
分析 (1)先求出私家车、地铁的速度,再求出小区与南禅寺距离即可.
(2)根据题意画出图象,在图中标出数据即可.
解答 解:(1)由图象可知,
私家车的速度为$\frac{22-11}{11}$=1千米/分钟,
地铁的速度为$\frac{22}{11}$=2千米/分钟,
小区与南禅寺相距2×11=22千米,
点A的实际意思是小颖乘地铁用11分钟到达南禅寺,此时与小明相距11千米,
故答案分别为22,1,2,小颖乘地铁用11分钟到达南禅寺,此时与小明相距11千米.
(2)S与t的函数图象如图所示,
22+30=52分钟,52分钟后小颖乘上了地铁,
52+5=57分钟,57分钟后小明的爸爸开始回家,此时小颖在小明的爸爸前面10千米,
57+(11-5)=63分钟时,小颖回到家中,此时两人相距16千米,
63+16=79分钟,79分钟时小明的爸爸到家.
点评 本题考查一次函数的应用,路程、速度、时间之间的关系等知识,解题的关键是读懂图象信息,学会画函数图象,属于中考常考题型.

练习册系列答案
相关题目
1.已知一次函数y=kx+b的图象经过(1,a)和(a,-1),其中a>1,则k,b的取值范围是( )
| A. | k>0,b>0 | B. | k<0,b>0 | C. | k>0,b<0 | D. | k<0,b<0 |
2.下列图形既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
12. 如图,直线AB和CD相交于点O,若∠AOD=134°,则∠AOC的度数为( )
如图,直线AB和CD相交于点O,若∠AOD=134°,则∠AOC的度数为( )
 如图,直线AB和CD相交于点O,若∠AOD=134°,则∠AOC的度数为( )
如图,直线AB和CD相交于点O,若∠AOD=134°,则∠AOC的度数为( )| A. | 134° | B. | 144° | C. | 46° | D. | 32° |
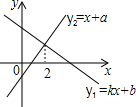 一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x<3时,y1<y2中,正确的序号是①.
一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x<3时,y1<y2中,正确的序号是①.