题目内容
5. 如图,已知抛物线y=ax2-x+c经过点Q (-2,4),且它的顶点P的横坐标为-1.设抛物线与x轴相交于A,B两点,
如图,已知抛物线y=ax2-x+c经过点Q (-2,4),且它的顶点P的横坐标为-1.设抛物线与x轴相交于A,B两点,(1)求抛物线的解析式;
(2)求A,B两点的坐标;
(3)设PB与y轴交于C点,求△ABC的面积.
分析 (1)根据Q坐标,以及顶点P坐标,列出关于a与c的方程组,求出方程组的解得到a与c的值,即可确定出抛物线解析式;
(2)对于抛物线解析式,令y=0,求出x的值,即可确定出A与B坐标;
(3)由P与B坐标,利用待定系数法确定出直线PB解析式,令x=0求出y的值,确定出OC的长,再由AB的长,求出三角形ABC面积即可.
解答 解:(1)把Q(-2,4)代入抛物线解析式得:4a+2+c=4①,
根据顶点坐标公式得:x=-$\frac{-1}{2a}$=-1,即a=-$\frac{1}{2}$②,
把②代入①得:c=4,
则抛物线解析式为y=-$\frac{1}{2}$x2-x+4;
(2)对于抛物线解析式为y=-$\frac{1}{2}$x2-x+4,
令y=0,得到-$\frac{1}{2}$x2-x+4=0,
整理得:x2+2x-8=0,即(x-2)(x+4)=0,
解得:x=2或x=-4,
则A(-4,0),B(2,0);
(3)设直线PB解析式为y=kx+b,
把P(-1,$\frac{9}{2}$),B(2,0)代入得:$\left\{\begin{array}{l}{-k+b=\frac{9}{2}}\\{2k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{3}{2}}\\{b=-3}\end{array}\right.$,
∴直线PB解析式为y=$\frac{3}{2}$x-3,
令x=0,得到y=-3,即C(0,-3),OC=3,
∵AB=2-(-4)=2+4=6,
∴S△ABC=$\frac{1}{2}$×AB×OC=9.
点评 此题考查了抛物线与x轴的交点,待定系数法确定二次函数解析式,熟练掌握待定系数法是解本题的关键.

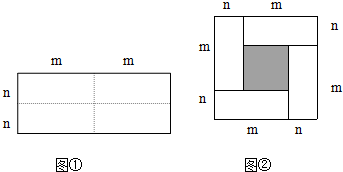
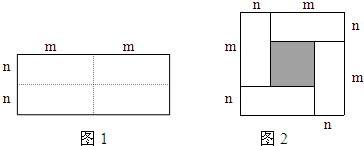
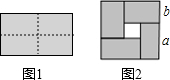 如图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积为( )
如图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积为( )| A. | ab | B. | (a+b)2 | C. | (a-b)2 | D. | a2-b2 |
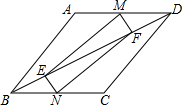 如图,已知平行四边形ABCD,点M,N分别在边AD和边BC上,点E,F在线段BD上,且AM=CN,DF=BE.求证:
如图,已知平行四边形ABCD,点M,N分别在边AD和边BC上,点E,F在线段BD上,且AM=CN,DF=BE.求证: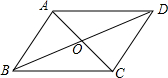 如图,在?ABCD中,已知AC、BD相交于点O,两条对角线的和为24cm,BC长为8cm,则△AOD的周长=20cm.
如图,在?ABCD中,已知AC、BD相交于点O,两条对角线的和为24cm,BC长为8cm,则△AOD的周长=20cm.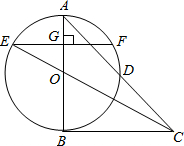 如图,在△ABC中,∠A=45°,以AB为直径的⊙O交于AC的中点D,连接CO,CO的延长线交⊙O于点E,过点E作EF⊥AB,垂足为点G.
如图,在△ABC中,∠A=45°,以AB为直径的⊙O交于AC的中点D,连接CO,CO的延长线交⊙O于点E,过点E作EF⊥AB,垂足为点G. 如图,在三角形ABC中,BE平分∠ABC,DE∥BC,则图中相等的角有5对.
如图,在三角形ABC中,BE平分∠ABC,DE∥BC,则图中相等的角有5对.