题目内容
9.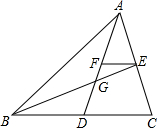 如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,那么$\frac{FG}{AG}$=$\frac{1}{4}$.
如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,那么$\frac{FG}{AG}$=$\frac{1}{4}$.
分析 由三角形的重心定理得出$\frac{EG}{BG}$=$\frac{1}{2}$,$\frac{DG}{AG}$=$\frac{1}{2}$,由平行线分线段成比例定理得出$\frac{FG}{DG}=\frac{EG}{BG}$=$\frac{1}{2}$,即可得出结果.
解答 解:∵线段AD、BE是△ABC的中线,
∴$\frac{EG}{BG}$=$\frac{1}{2}$,$\frac{DG}{AG}$=$\frac{1}{2}$,
∵EF∥BC,$\frac{FG}{DG}=\frac{EG}{BG}$=$\frac{1}{2}$,
∴$\frac{FG}{AG}$=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查了平行线分线段成比例定理、三角形的重心定理;熟练掌握三角形的重心定理,由平行线分线段成比例定理得出FG:DG=1:2是解决问题的关键

练习册系列答案
相关题目
17.若a=$\sqrt{2}$-1,b=$\sqrt{2}$+1,则代数式a2-b2的值是( )
| A. | 4$\sqrt{2}$ | B. | 3 | C. | -3 | D. | -4$\sqrt{2}$ |
4.如果△ABC∽△DEF,相似比为2:1,且△DEF的面积为4,那么△ABC的面积为( )
| A. | 1 | B. | 4 | C. | 8 | D. | 16 |
17.四个有理数2、1、0、-1,其中最小的是( )
| A. | 1 | B. | 0 | C. | -1 | D. | 2 |
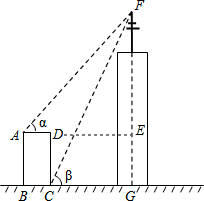 如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A,C两点测得该塔顶端F的仰角分别为和β,矩形建筑物宽度AD=20m,高度DC=33m.求:
如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A,C两点测得该塔顶端F的仰角分别为和β,矩形建筑物宽度AD=20m,高度DC=33m.求: