题目内容
14.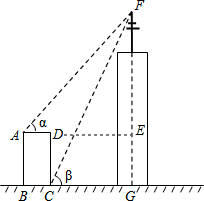 如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A,C两点测得该塔顶端F的仰角分别为和β,矩形建筑物宽度AD=20m,高度DC=33m.求:
如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A,C两点测得该塔顶端F的仰角分别为和β,矩形建筑物宽度AD=20m,高度DC=33m.求:(1)试用α和β的三角比表示线段CG的长;
(2)如果α=48°,β=65°,请求出信号发射塔顶端到地面的高度FG的值.(结果精确到1m)(参考数据:sin48°=0.7,cos48°=0.7,tan48°=1.1,sin65°=0.9,cos65°=0.4,tan65°=2.1)
分析 (1)将题目中所涉及到的仰角转换为直角三角形的内角,利用解直角三角形的知识表示出线段CG的长即可.
(2)根据三角函数值求得CG的长,代入FG=x•tanβ即可求得.
解答 解:(1)设CG=xm,
由图可知:EF=(x+20)•tanα,FG=x•tanβ,
则(x+20)tanα+33=xtanβ,
解得x=$\frac{33+20tanα}{tanβ-tanα}$;
(2)x=$\frac{33+20tanα}{tanβ-tanα}$=$\frac{33+20×1.1}{2.1-1.1}$=55,
则FG=x•tanβ=55×2.1=115.5≈116.
答:该信号发射塔顶端到地面的高度FG约是116m.
点评 本题考查了仰角问题,解决此类问题的关键是正确的将仰角转化为直角三角形的内角并选择正确的边角关系解直角三角形.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
4.小黄做一道题“已知两个多项式A,B,计算A-B”.小黄误将A-B看作A+B,求得结果是9x2-2x+7.若B=x2+3x-2,请你帮助小黄求出A-B的正确答案( )
| A. | 8x2-5x+9 | B. | 7x2-8x+11 | C. | 10x2+x+5 | D. | 7x2+4x+3 |
5.已知反比例函数y=$\frac{6}{x}$,下列各点不在该函数图象上的是( )
| A. | (2,3) | B. | (-2,-3) | C. | (2,-3) | D. | (1,6) |
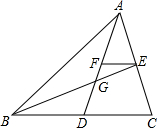 如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,那么$\frac{FG}{AG}$=$\frac{1}{4}$.
如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,那么$\frac{FG}{AG}$=$\frac{1}{4}$. 如图,一长方体底面宽AN=5cm,长BN=10cm,高BC=16cm.D为BC的中点,一动点P从A点出发,在长方体表面移动到D点的最短距离是$\sqrt{289}$cm.
如图,一长方体底面宽AN=5cm,长BN=10cm,高BC=16cm.D为BC的中点,一动点P从A点出发,在长方体表面移动到D点的最短距离是$\sqrt{289}$cm.